354342IO. BAPT. BENED.
Alia etiam via poſſumus idem concludere.
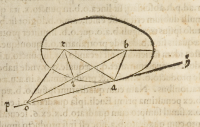
Imaginemur maiorem axem alicu-
ius ellipſis tranſire per duo puncta .r. et .b. ſupponendo ipſa puncta, ea eſle, quæ ita
axem diuidunt, vt ſingula produ-
 385[Figure 385]
cta fectionum ſint, vt inquit Per-
385[Figure 385]
cta fectionum ſint, vt inquit Per-
geus. imaginemur, etiam .p.h. con
tiguam eſſe ipſi ellipſi in puncto .a.
vnde ſi protractæ fuerint duæ .r.a.
et .b.a. habebimus ex .48. tertijip-
ſius Pergei angulos .b.a.h. et .r.a.
p. inuicem æquales. Ducendo
poſtea ad quoduis punctum ipſius
p.h. duas .b.o. et .r.o. certi erimus,
quod ſecabuntur à gyro oxygo-
nio, quarum vna ſecta ſit in pun-
cto .i. ducta poſtea .i.r. clarum erit ex .52. dicti, quod longitudo .b.i.r. æqualis erit lon
gitudini .b.a.r. & minor ipſa .b.o.r. ex .21. primi Euclid.
ius ellipſis tranſire per duo puncta .r. et .b. ſupponendo ipſa puncta, ea eſle, quæ ita
axem diuidunt, vt ſingula produ-
geus. imaginemur, etiam .p.h. con
tiguam eſſe ipſi ellipſi in puncto .a.
vnde ſi protractæ fuerint duæ .r.a.
et .b.a. habebimus ex .48. tertijip-
ſius Pergei angulos .b.a.h. et .r.a.
p. inuicem æquales. Ducendo
poſtea ad quoduis punctum ipſius
p.h. duas .b.o. et .r.o. certi erimus,
quod ſecabuntur à gyro oxygo-
nio, quarum vna ſecta ſit in pun-
cto .i. ducta poſtea .i.r. clarum erit ex .52. dicti, quod longitudo .b.i.r. æqualis erit lon
gitudini .b.a.r. & minor ipſa .b.o.r. ex .21. primi Euclid.
Deerrore Euclidis circa ſpeculum vstorium.
AD EVNDEM.
VErum ſpeculum vſtorium, illud non eſt, quod ab Euclide traditum fuit, & quod
tu etiam putas, Nam Euclides errat, cum credat radios reflexos à ſuperficie
ſphærica concaua ſeinuicem in centro ſpeculi interſecare. Nam cum omnes lineę
recte à centro, & cir cunferentia alicuius ſphæræ terminatæ, ſint eidem circunferen-
tiæ perpendiculares, ſequeretur ex neceſſitate radios incidentiæ etiam perpendicu
lares eidem ſuperficiei eſſe, cum anguli incidentiæ ſemper æquales ſint angulis re-
flexionis, vnde etiam ex neceſſitate ſequeretur punctum corporis lucidi, à quo radij
luminoſi excunt, in centro ſpeculi reperiri. quod quidem falſiſſimum eſt.
tu etiam putas, Nam Euclides errat, cum credat radios reflexos à ſuperficie
ſphærica concaua ſeinuicem in centro ſpeculi interſecare. Nam cum omnes lineę
recte à centro, & cir cunferentia alicuius ſphæræ terminatæ, ſint eidem circunferen-
tiæ perpendiculares, ſequeretur ex neceſſitate radios incidentiæ etiam perpendicu
lares eidem ſuperficiei eſſe, cum anguli incidentiæ ſemper æquales ſint angulis re-
flexionis, vnde etiam ex neceſſitate ſequeretur punctum corporis lucidi, à quo radij
luminoſi excunt, in centro ſpeculi reperiri. quod quidem falſiſſimum eſt.
Alia etiam via poſſum hanc oſtendere impoſſibilitatem, & tibi probabo, quod
in nullo aliquo puncto poſſunt inuicem conuenire ipſi radijrefle xi omnes.
in nullo aliquo puncto poſſunt inuicem conuenire ipſi radijrefle xi omnes.
Sit igitur .l.a.c. conis ſectio ſuperficiei reflexionis cum ſpeculo, cuius centrum ſit .o.
punctum verò lucidum ſit .g. protrahaturque .g.o.a. Nunc autem primum dico, quod
radij reflexi à punctis diuerſarum diſtantiarum ab .a. non coincident inuicem in aliquo
puncto lineę .g.o.a: ſint ergo duo puncta .u. et .r. diuerſarum diſtantiarum ab .a. à quibus
veniant duo radij incidentiæ .g.r. et .g.u. radius verò reflexus ab .r. ſit .r.e. protrahatur
u.e. quam dico effe non poſſe radium reflexum ab .u. quotieſcunque eius incidens
deſcendat ab .g. Protrahantur ergo duæ lineæ .o.r. et .o.u. vnde cum dixerit aliquis
u.e. reflexum eſſe ipſius .g.u. igitur anguli .g.u.o. et .o.u.e. erunt inuicem æquales, & ſic
etiam erunt duo .g.r.o. et .o.r.e. vnde ex tertia ſexti & .11. quinti Eucli. proportio .g.
u. ad .u.e. æqualis eſſet ei, quæ .g.r. ad .r.e. quod quidem impoſſibile eſſe demonſtra-
bo, eo quod cum .g.u. maior ſit .g.r. ex .8. tertij, erit ex .8. quinti proportio ipſius .g.u.
ad .r.e. maior proportione ipſius .g.r. ad .r.e. ſed ex .7. tertij .u.e. minor eſt .r.e. erit igi-
tur ex dicta .8. quinti maior proportio ipſius .g.u. ad .u.e. quam .g.u. ad .r.e. vnde eo ma
punctum verò lucidum ſit .g. protrahaturque .g.o.a. Nunc autem primum dico, quod
radij reflexi à punctis diuerſarum diſtantiarum ab .a. non coincident inuicem in aliquo
puncto lineę .g.o.a: ſint ergo duo puncta .u. et .r. diuerſarum diſtantiarum ab .a. à quibus
veniant duo radij incidentiæ .g.r. et .g.u. radius verò reflexus ab .r. ſit .r.e. protrahatur
u.e. quam dico effe non poſſe radium reflexum ab .u. quotieſcunque eius incidens
deſcendat ab .g. Protrahantur ergo duæ lineæ .o.r. et .o.u. vnde cum dixerit aliquis
u.e. reflexum eſſe ipſius .g.u. igitur anguli .g.u.o. et .o.u.e. erunt inuicem æquales, & ſic
etiam erunt duo .g.r.o. et .o.r.e. vnde ex tertia ſexti & .11. quinti Eucli. proportio .g.
u. ad .u.e. æqualis eſſet ei, quæ .g.r. ad .r.e. quod quidem impoſſibile eſſe demonſtra-
bo, eo quod cum .g.u. maior ſit .g.r. ex .8. tertij, erit ex .8. quinti proportio ipſius .g.u.
ad .r.e. maior proportione ipſius .g.r. ad .r.e. ſed ex .7. tertij .u.e. minor eſt .r.e. erit igi-
tur ex dicta .8. quinti maior proportio ipſius .g.u. ad .u.e. quam .g.u. ad .r.e. vnde eo ma

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib