356344IO. BAPT. BENED.
refleyus ſecabit cathetum .b.o. in puncto .c. intra ſpeculum, nec dubitandum eſt quin
linea .e.b. ſectura ſit .b.o. eo quod cum angulus .o.e.c. ſit maior angulo .e.o.c. ex .19.
primi, & ſimiliter angulus .b.e.f. ſequitur ex .13. dicti, angulos .b.e.o. et .e.o.b. eſſe mi
nores duobus rectis, vnde ex penultima petitione primi, duæ lineæ .b.e. et .o.b. inuicem
concurrent. Quare poſſumus ex hoc, quoddam corollarium extrahere, hoc eſt
neceſſarium semper exiſtat, vt linea .c.e. minor eſſe linea .c.o. Sed vnde eueniat quod ip
ſa neceſſariò debeat ſemper maior eſſe ipſa .c.g. clarum eſt ex .7. tertij Eucli. Nunc
imaginemur ductas eſſe duas tangentes .b.d. et .b.h. & ab .e. ipsam .e.i. vnde certi erimus,
quod ab interuallo inter .h. et .d. punctum .b. ponſſibile ſit vt reflectatur. Accipiamus
nunc .p.c. minorem medietate ipſius .b.c. & à puncto .p. imaginemur tangentem .p.q.
in puncto .q. prorractaq́ue ſit .b.q. vt radius incidentiæ, tunc dico, radium reflexum
ipſius .b.q. non concurrere in eodem puncto .c. ipſius catheti, ſi vero dixeris quod ſic. Eſto
igitur radius dictus .c.q.s. Imaginemur tangentem .e.i. in puncto .e. vnde ex .18. quinti Alha
zem, vel .12. ſexti Vitellionis proportio .b.i. ad .i.c. erit, vt .b.o. ad .o.c. & ſimiliter erit
ipſius .b.p. ad .p.c. vt .b.o. ad .o.c. ex eadem. Quare ex .11. quinti Eucli. proportio ip
ſius .b.p. ad .p.c. erit vt ipſius .b.i. ad .i.c. ſed quia .p.b. vt pars ipſius .b.i. minor eſt ip-
ſa, ergo ex .14. dicti .p.c. minor erit ipſa .c.i. hoc eſt totum minus ſua parte, quod eſt
impoſſibile, quare non in ipſo catheto videbitur imago ipſius obiecti.
linea .e.b. ſectura ſit .b.o. eo quod cum angulus .o.e.c. ſit maior angulo .e.o.c. ex .19.
primi, & ſimiliter angulus .b.e.f. ſequitur ex .13. dicti, angulos .b.e.o. et .e.o.b. eſſe mi
nores duobus rectis, vnde ex penultima petitione primi, duæ lineæ .b.e. et .o.b. inuicem
concurrent. Quare poſſumus ex hoc, quoddam corollarium extrahere, hoc eſt
neceſſarium semper exiſtat, vt linea .c.e. minor eſſe linea .c.o. Sed vnde eueniat quod ip
ſa neceſſariò debeat ſemper maior eſſe ipſa .c.g. clarum eſt ex .7. tertij Eucli. Nunc
imaginemur ductas eſſe duas tangentes .b.d. et .b.h. & ab .e. ipsam .e.i. vnde certi erimus,
quod ab interuallo inter .h. et .d. punctum .b. ponſſibile ſit vt reflectatur. Accipiamus
nunc .p.c. minorem medietate ipſius .b.c. & à puncto .p. imaginemur tangentem .p.q.
in puncto .q. prorractaq́ue ſit .b.q. vt radius incidentiæ, tunc dico, radium reflexum
ipſius .b.q. non concurrere in eodem puncto .c. ipſius catheti, ſi vero dixeris quod ſic. Eſto
igitur radius dictus .c.q.s. Imaginemur tangentem .e.i. in puncto .e. vnde ex .18. quinti Alha
zem, vel .12. ſexti Vitellionis proportio .b.i. ad .i.c. erit, vt .b.o. ad .o.c. & ſimiliter erit
ipſius .b.p. ad .p.c. vt .b.o. ad .o.c. ex eadem. Quare ex .11. quinti Eucli. proportio ip
ſius .b.p. ad .p.c. erit vt ipſius .b.i. ad .i.c. ſed quia .p.b. vt pars ipſius .b.i. minor eſt ip-
ſa, ergo ex .14. dicti .p.c. minor erit ipſa .c.i. hoc eſt totum minus ſua parte, quod eſt
impoſſibile, quare non in ipſo catheto videbitur imago ipſius obiecti.
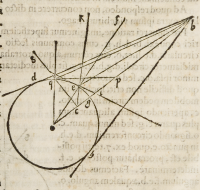
Aliud notandum etiam cernere potes ex ipſis ſpeculis ſphæricis conuexis, hoc eſt
quod poſſibile ſit aliquoties, radium reflexum concurrere cum catheto incidentiæ
extra ſpeculum inter puncta .g. et .p. vt exempli gratia .ſi punctus .p. eſſet exactè
in medio inter .b. et g. tunc punctum .c. ipſius concurſus cum catheto incidentiæ eſſet
inter .g. et .p. eo quod cum linea .p.q. debeat @iui lere angulum .b. q, c. per ęqualia, oportebit
c. poſitum eſſe inter .g. et .p. quia angulus .g.q.p. maior eſt angulo .p.q.b. vt per te faci
le potes ratiotinari, imaginando cir
 388[Figure 388]
culum circa triangulum .g.q.b. & dia
388[Figure 388]
culum circa triangulum .g.q.b. & dia
merrum perpendicularem .ad .g.b.
in puncto .p. producendo poſtea .q.
p. vſque; ad alteram partem circunferen-
tiæ ipſius circuli. argumentando dein-
de mediante vltima ſexti, illud idem
po@es etiam ſcire ex .22. quinti Alha
zeni. & ex .26. ſexti Vitellionis. vn-
de ſi ad ambas pupillas venerint ra
dij reflexi ipſius obiecti .b.a. duobus
punctis huiuſmodi ſpeculi, ita di-
ſtantibus à puncto .g. vt .q. tunc com
mune punctum concurſus axium vi
ſualium erit in catheto inter .g.p.
vbi apparebit imago ex ſuperius di
ctis rationibus, ita vt non ſolum con
cauis, ſed etiam conuexis hoc accidere poſſit.
quod poſſibile ſit aliquoties, radium reflexum concurrere cum catheto incidentiæ
extra ſpeculum inter puncta .g. et .p. vt exempli gratia .ſi punctus .p. eſſet exactè
in medio inter .b. et g. tunc punctum .c. ipſius concurſus cum catheto incidentiæ eſſet
inter .g. et .p. eo quod cum linea .p.q. debeat @iui lere angulum .b. q, c. per ęqualia, oportebit
c. poſitum eſſe inter .g. et .p. quia angulus .g.q.p. maior eſt angulo .p.q.b. vt per te faci
le potes ratiotinari, imaginando cir
merrum perpendicularem .ad .g.b.
in puncto .p. producendo poſtea .q.
p. vſque; ad alteram partem circunferen-
tiæ ipſius circuli. argumentando dein-
de mediante vltima ſexti, illud idem
po@es etiam ſcire ex .22. quinti Alha
zeni. & ex .26. ſexti Vitellionis. vn-
de ſi ad ambas pupillas venerint ra
dij reflexi ipſius obiecti .b.a. duobus
punctis huiuſmodi ſpeculi, ita di-
ſtantibus à puncto .g. vt .q. tunc com
mune punctum concurſus axium vi
ſualium erit in catheto inter .g.p.
vbi apparebit imago ex ſuperius di
ctis rationibus, ita vt non ſolum con
cauis, ſed etiam conuexis hoc accidere poſſit.
In planis autem nunquam hoc poteſt euenire, vt tibi alias dixi, eo quod ſi acceperi-
mus rectam .m.r. pro coni ſectione ſuperficiei .l.t.x. reflexionis & ſuperficiei ſpeculi, punctumque;
lucidum .l. protractoque; catheto .l.r.t. lineisque; incidentiæ .l.x. et .l.m. reflexionis etiam
x.y. et .m.z. cum anguli .l.x.r. et .y.x.h. et .r.x.t. æquales inuicem ſint, & ſic anguli .l.m.
r. et .z.m.h. et .r.m.t. erit .r.t. tam pro triangulo .r.x.t. quam pro triangulo .r.m.t. æqua
lis .r.l. ex .26. primi, ita quod ſemper in puncto .t. conuenient omnes radij reflexi ipſius
mus rectam .m.r. pro coni ſectione ſuperficiei .l.t.x. reflexionis & ſuperficiei ſpeculi, punctumque;
lucidum .l. protractoque; catheto .l.r.t. lineisque; incidentiæ .l.x. et .l.m. reflexionis etiam
x.y. et .m.z. cum anguli .l.x.r. et .y.x.h. et .r.x.t. æquales inuicem ſint, & ſic anguli .l.m.
r. et .z.m.h. et .r.m.t. erit .r.t. tam pro triangulo .r.x.t. quam pro triangulo .r.m.t. æqua
lis .r.l. ex .26. primi, ita quod ſemper in puncto .t. conuenient omnes radij reflexi ipſius

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib