3725THEOREM. ARIT.
noni, hocque; rectangulum .g.r. quadratum eſt primi numeri propoſiti ex .19. theo-
remate huius libri, itaque; cognitum erit. vnà etiam gnomon .u.g.t. cognoſcetur,
quare totum quadratum .g.y. eiusque; radix .b.g. manifęſta erit, cui coniuncta .q.b.
data, maius quadratum .q.g. cognoſcetur, ex qua .b.g. detracta .b.i. data, cogno-
ſcetur .i.g. quadratum minus conſequenter, etiam eorum radices notæ erunt.
remate huius libri, itaque; cognitum erit. vnà etiam gnomon .u.g.t. cognoſcetur,
quare totum quadratum .g.y. eiusque; radix .b.g. manifęſta erit, cui coniuncta .q.b.
data, maius quadratum .q.g. cognoſcetur, ex qua .b.g. detracta .b.i. data, cogno-
ſcetur .i.g. quadratum minus conſequenter, etiam eorum radices notæ erunt.
THEOREMA XXXIX.
ALia etiam ratione idipſum definiri poteſt, prætermiſſa antiquorum via,
nempe multiplicatis in ſemetipſis primo & ſecundo, numeris propoſitis, qua-
druplicatoque; quadrato primi, qua ſumma coniuncta cum quadrato ſecundi nume-
ri, & ex hac altera ſumma eruta radice quadrata, ex qua detracto ſecundo nume-
ro, & è reliquo ſumpto dimidio, quod erit quadratum minus, quo detracto ex radi-
ce poſtremo iuncta, ſupererit quadrarum maius.
nempe multiplicatis in ſemetipſis primo & ſecundo, numeris propoſitis, qua-
druplicatoque; quadrato primi, qua ſumma coniuncta cum quadrato ſecundi nume-
ri, & ex hac altera ſumma eruta radice quadrata, ex qua detracto ſecundo nume-
ro, & è reliquo ſumpto dimidio, quod erit quadratum minus, quo detracto ex radi-
ce poſtremo iuncta, ſupererit quadrarum maius.
Exempli gratia, ſi proponeretur numerus .8. cui productum duorum numerorum
quæſitorum æquandum eſt, proponeretur idem .12. cui differentia quadratorum
duorum numerorum æqualis eſſe debet. Iubeo primum numerum, nempe .8. in ſe
ipſum multiplicari, ex quo exurget .64. pro numero ſui quadrati, quod quadru-
plicari volo, eritque; productum .256. quod cenſeo coniungendum cum quadrato ſe-
cundi numeri propoſiti, nempe .144. eritque; ſumma .400. ex quaſumetur radix, ſci
licet .20. & ex hac detrahetur ſecundus numerus .12. reſiduique; dimidium, nempe .
4. pro quadrato minore, quo in ſummam collecto cum, 12. dabit quadratum
maius .16.
quæſitorum æquandum eſt, proponeretur idem .12. cui differentia quadratorum
duorum numerorum æqualis eſſe debet. Iubeo primum numerum, nempe .8. in ſe
ipſum multiplicari, ex quo exurget .64. pro numero ſui quadrati, quod quadru-
plicari volo, eritque; productum .256. quod cenſeo coniungendum cum quadrato ſe-
cundi numeri propoſiti, nempe .144. eritque; ſumma .400. ex quaſumetur radix, ſci
licet .20. & ex hac detrahetur ſecundus numerus .12. reſiduique; dimidium, nempe .
4. pro quadrato minore, quo in ſummam collecto cum, 12. dabit quadratum
maius .16.
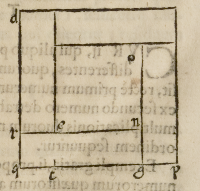
Cuius ſpeculationis cauſa, quadratum maius per lineam .q.g. minus per .g.p. ſi-
gnificetur: ſuper integram autem .q.p. erigatur quadratum integrum .d.p. diuiſum,
vt quadratum .f.g. vigeſimiſeptimi theorematis huius libri, (idipſum accideret di-
uiſo quadrato modo octauæ ſecundi Euclidis) quæ quidem diuiſio, eſt via quatuor
productorum .q.g. in .g.p. è quibus vnum ſit .g.r. quod erit cognitum ex .19. theore
mate cum ſit quadratum primi numeri ppoſiti, ex quo illa quatuor cognita erunt. Iam
verò ſi cogitemus .q.p. ſectam in puncto .t. ita vt .q.t. æqualis ſit .p.g. dabitur differen
tia .t.g. cognita, vt radix quadrati .e.o. cum ex præſup-
poſito .r.n. æqualis ſit .q.g. et .r.e: g.p. ex quo etiam .q.t.
 52[Figure 52]
ita pariter .e.n.t.g. æqualis erit.
Collecto itaque; quadra
52[Figure 52]
ita pariter .e.n.t.g. æqualis erit.
Collecto itaque; quadra
to .e.o. ipſius .t.g. cum quadruplo .g.r: cognitum erit
quadratum .d.p. ipſius .q.p. quare cognoſcetur .q.p. de
quo numero detracta differétia quadratorum cognita .
t.g. ſupererit aggregatum .p.g. et .q.t. cognitum. Qua-
re ex conſequenti, dimidium aggregati, nempe .g.p.
cognoſcetur, tanquam minus duorum quadratorum.
cui iuncta .g.t. aut detracta .p.g. ex .p.q. quadratum .q.
g. maius cognitum remanebit.
gnificetur: ſuper integram autem .q.p. erigatur quadratum integrum .d.p. diuiſum,
vt quadratum .f.g. vigeſimiſeptimi theorematis huius libri, (idipſum accideret di-
uiſo quadrato modo octauæ ſecundi Euclidis) quæ quidem diuiſio, eſt via quatuor
productorum .q.g. in .g.p. è quibus vnum ſit .g.r. quod erit cognitum ex .19. theore
mate cum ſit quadratum primi numeri ppoſiti, ex quo illa quatuor cognita erunt. Iam
verò ſi cogitemus .q.p. ſectam in puncto .t. ita vt .q.t. æqualis ſit .p.g. dabitur differen
tia .t.g. cognita, vt radix quadrati .e.o. cum ex præſup-
poſito .r.n. æqualis ſit .q.g. et .r.e: g.p. ex quo etiam .q.t.
to .e.o. ipſius .t.g. cum quadruplo .g.r: cognitum erit
quadratum .d.p. ipſius .q.p. quare cognoſcetur .q.p. de
quo numero detracta differétia quadratorum cognita .
t.g. ſupererit aggregatum .p.g. et .q.t. cognitum. Qua-
re ex conſequenti, dimidium aggregati, nempe .g.p.
cognoſcetur, tanquam minus duorum quadratorum.
cui iuncta .g.t. aut detracta .p.g. ex .p.q. quadratum .q.
g. maius cognitum remanebit.
THEOREMA XL.
CVR ijs, qui volunt duos eiuſmodi numeros inuenire, vt eorum maior mi-
norem, numero propoſito ſuperet, & productum vnius in alterum, alteri nu-
mero propoſito adęquetur, conſultiſsimum ſit dimidium primi numeri propoſiti,
norem, numero propoſito ſuperet, & productum vnius in alterum, alteri nu-
mero propoſito adęquetur, conſultiſsimum ſit dimidium primi numeri propoſiti,

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib