Benedetti, Giovanni Battista de - Io. Baptistae Benedicti ... Diversarvm specvlationvm mathematicarum, et physicarum liber : quarum seriem sequens pagina indicabit ; [annotated and critiqued by Guidobaldo Del Monte]

Scan	Original
41	29
42	30
43	31
44	32
45	33
46	34
47	35
48	36
49	37
50	38
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58

5038IO. BAPT. BENED.

Hoc vt demonſtremus, primus nu-

67[Figure 67] merus linea .a.b. ſignificetur, quam di-
uiſam cogitemus in puncto .c. in partes
quæſitas, ex quo præſupponitur duas li-
neas .a.c. et .c.b. duo quadrata eſſe, quæ
in altera figura ſignificetur per .d. et .e.
productum autem radicum cognitum .
f. quandoquidem datum eſt, cuius qua-
dratum æquale erit producto quadra-
torum .d.e. adinuicem, nempe .b.c. in .a.c. ex .19. theoremate huius. Quod verbi
gratia ſit .x. itaque; cognitum, quo facto, doctrinam .45. theorematis libri huius ſecuti,
propoſitum conſequemur.

THEOREMA LX.

CVR productum differentiæ duarum radicum in ſummam ipſarum, ſemper
differentia ſit quadratorum ipſarum radicum.

Exempli gratia, quoslibet duos numeros pro radicibus ſumpſerimus, vt potè .3. et .
5. quorum differentia eſt .2. certè ſi differentiam hanc per ſummam radicum ſcili-
cet .8. multiplicauerimus, dabitur numerus .16. quod productum differentia eſt
ſuorum quadratorum, nempeinter .9. et .25.

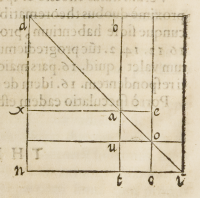
Hoc vt ſpeculemur, duæ radices in linea .n.i. ſignificentur, quarum vna ſit .n.c. &
altera .c.i. ipſarum autem differentia .n.t. ex quo .t.
c. æqualis erit .c.i. Tum cogitato toto quadrato .d.i.

68[Figure 68] cum diametro .d.i. ductaque parallela lateri .n.d. à
puncto .c. & altera à puncto .t. & à puncto .o. tertia
ipſi .n.i. & à puncto .a. quarta .x.a.e. parallela ipſi .
o. inueniemus .b.n. productum eſſe differentiæ .n.
t. in ſumma radicum .n.i. & cum .d.o. et .a.o. ſint
quadrata radicum prædictarum: b.e. æquale erit .
n.u. cum vtrunque horum productorum æquale ſit .
x.u. ex quo gnomon .e.d.u. æqualis erit producto .
b.n. quod ſcire cupiebamus.

THEOREMA LXI.

CVR propoſitum aliquem numerum diuiſuri in duas eiuſmodi partes, vt diffe-
rentia radicum quadratarum æqualis ſit alteri numero propoſito, cuius ta-
men quadratum dimidij primi quadratum non excedat. Rectè ſecundum numerum
in ſeipſum multiplicant, productum verò ex primo numero detrahunt, rurſusque; di
midium reſidui quadrant, & quadratum hoc ex quadrato dimidij primi ſubtrahunt,
atque ita radice quadrata reſidui, dimidio primi coniuncta, pars maior datur, qua
ex ipſo dimidio detracta, pars minor relinquitur.

Exempli gratia, propoſito numero .20. ita ut propoſitum eſt, diuidendo, nem-
pe vt differentia radicum quadratarum dictarum partium æqualis ſit binario, bina-
rium hocin ſeipſum multiplicabimus, cuius quadratum .4. è primo numero .20. de

Page concordance

Text layer

Text normalization

Search

Scan	Original
41	29
42	30
43	31
44	32
45	33
46	34
47	35
48	36
49	37
50	38
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58

Scan	Original
41	29
42	30
43	31
44	32
45	33
46	34
47	35
48	36
49	37
50	38
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58

Scan	Original
41	29
42	30
43	31
44	32
45	33
46	34
47	35
48	36
49	37
50	38
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58