Benedetti, Giovanni Battista de - Io. Baptistae Benedicti ... Diversarvm specvlationvm mathematicarum, et physicarum liber : quarum seriem sequens pagina indicabit ; [annotated and critiqued by Guidobaldo Del Monte]

Scan	Original
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70
81	71
82	70
83	71
84	72
85	73
86	74
87	75
88	76
89	77
90	78

6755THEOR. ARITH. æqualis .e: et .q.n. æqualis .i. Nunc co-

92[Figure 92] gitemus abſolui corpus .n.h. ita ut .b.
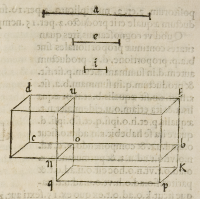
o.c.ſit vnica recta linea, ex quo ex .25.
vndecimi proportio .n.h. ad .n.k. ea-
dem eſt quæ .o.h. ad o.k. ſed ſic ſe ha-
bet .o.h. ad .o.k. vt .h.b. ad .b.k.
ex prima ſexti aut .18. vel .19. ſe-
ptimi itaque .n.h. ad .n.k. ex .11.
quinti ſic ſe habebit. vt .h.b. ad .b.k.
ſed .n.h. ad .n.d. ex eiſdem ſic ſe habet
ut .h.u. ad .d.u. et .h.u. ad .u.d. ita ut .h.
b. ad .b.k. ex præſuppoſito. Itaque ex
11. prædicta .n.h. ad .n.k. eadem erit
proportio quæ .n.h. ad .n.d. Quare
ex .9. quinti .n.k. æqualis erit .n.d.
Quod erat propoſitum.

THEOREMA LXXXIIII.

CVR quadrato vnius quantitatis radice proportionalis, per ſingulos tres termi
nos diuiſo, prouenientia, ſingulis dictis terminis ſint æqualia.

Exempli gratia, datis tribus terminis continuis proportionalibus .9. 6. 4. qua
dratum medij erit .36. quod per .9. diuiſum dabit .4: per .6: 6. per .4: 9.

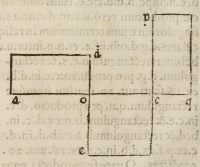
Cuius gratia, ſint tres termini continui proportionales .a.o: o.c. et .c.q. quadratum autem
medij ſit .e.c. Iam ſi applicetur rectangulum .a.d. æquale quadrato .e.c. ipſi .a.o. & re-
ctangulum .q.p. æquale eidem quadrato .e.c. ipſi .c.q. ſi quadratum .e.c. per .a.o. diui
ſerimus, proueniens erit .o.d. diuiſoque per .c.q. proueniens erit .c.p. quod ſi per ſuam
radicem .o.c. diuidatur, proueniens erit .o.

93[Figure 93] e. quod ſine dubio æquale eſt .o.c. ſed dico .
o.d. æqualem eſſe .c.q. Nam ex .16. ſexti aut
20. ſeptimi eadem eſt proportio .a.o. ad .o.
c. quę .o.e. ad .o.d. nempe .o.c. ad .o.d. itaque
o.d. ex .9. quinti æqualis eſt .c.q. quandoqui
dem ex .11. ſic ſe habet .o.c. ad .o.d. ſicut .o.
c. ad .c.q. Applicatis ijſdem rationibus ipſi .
p.c. probabimus .c.p. æqualem eſſe .a.o. cum
o.c. media ſit proportionalis, tam inter .c.p. et
c.q. quam inter .a.o. et .c.q. itaque .c.p. æqua-
lis eſt .a.o.

THEOREMA LXXXV.

CVR propoſitis tribus quantitatibus continuis proportionalibus proportione
aliarum duarum nobis datarum, multiplicata maiori poſtremarum dua-
rum in ſummam mediæ cum minima trium primarum, productum æqua-
le ſit producto minoris duarum in ſummam maximæ cum media trium.

Exempli gratia proponuntur quantitates .9. 6. 4. proportione numerorum pro-

Page concordance

Text layer

Text normalization

Search

Scan	Original
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70
81	71
82	70
83	71
84	72
85	73
86	74
87	75
88	76
89	77
90	78

Scan	Original
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70
81	71
82	70
83	71
84	72
85	73
86	74
87	75
88	76
89	77
90	78

Scan	Original
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70
81	71
82	70
83	71
84	72
85	73
86	74
87	75
88	76
89	77
90	78