7159THEOREM. ARIT.
eſſe gnomoni .e.c.u. itemque; gnomonem .b.f.d. æqualem gnomoni .b.o.d. at hic gno-
mon .b.o.d. ex præſuppoſito, maior eſt gnomone .e.o.u. duabus vnitatibus .b. et .d.
Itaque etiam gnomon .b.f.d. duabus vnitatibus gnomonem .e.c.u. ſuperabit. Qua-
re .b.f.d. erit impar immediatè ſequens ternarium, qui coniunctus quadrato .o.c.
quadratum ſubſequens componet. Eadem ratione probabitur de quadrato .o.n. ſe
quenti .o.f. & gnomone .i.n.a. cum hic ordo ſpeculationis ſit vniuerſalis. In
quo cernitur quemlibet gnomonem ſibi contiguum inferiorem ſemper duabus vni-
tat ibus excedere, cumque quadrata non niſi gnomonibus ſibi inuicem ſuccedant.
Sed cum primus .e.c.u. diſpar fuerit, proculdubio etiam neceſſarioque; cæteri diſpares erunt.
Ex qua ſpeculatione, oritur regula ab antiquis tradita
inueniendi vltimi numeri diſparis concurrentis ad compo
ſitionem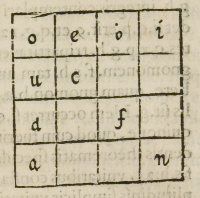 99[Figure 99]
compo
99[Figure 99]
compo
ſitionem alicuius quadrati. Vt ſi quis ſeire deſideret nu-
merum vltimum diſparem, quo mediante quadratum .
o.n. conſtitutum fuit, quod aliud non eſt quam ſcire
quantus ſit numerus vltimi gnomonis .i.n.a. æqualis gno
moni .i.o.a. Itaque vt ſciamus hunc gnomonem .i.o.a.
patet duplicandam eſſe radicem .o.e.b.i. dabiturque, .o.e.
b.i. et .o.u.d.a. vbi bis reperitur .o. nos autem tantummo
do quærimus ſcire gnomonem .i.b.e.o.u.d.a. Itaque
minor eſt vnitate duplo radicis, cum unitas .o. bis repe-
tatur, quæ tamen in gnomone ſemel tantum ſumebatur.
mon .b.o.d. ex præſuppoſito, maior eſt gnomone .e.o.u. duabus vnitatibus .b. et .d.
Itaque etiam gnomon .b.f.d. duabus vnitatibus gnomonem .e.c.u. ſuperabit. Qua-
re .b.f.d. erit impar immediatè ſequens ternarium, qui coniunctus quadrato .o.c.
quadratum ſubſequens componet. Eadem ratione probabitur de quadrato .o.n. ſe
quenti .o.f. & gnomone .i.n.a. cum hic ordo ſpeculationis ſit vniuerſalis. In
quo cernitur quemlibet gnomonem ſibi contiguum inferiorem ſemper duabus vni-
tat ibus excedere, cumque quadrata non niſi gnomonibus ſibi inuicem ſuccedant.
Sed cum primus .e.c.u. diſpar fuerit, proculdubio etiam neceſſarioque; cæteri diſpares erunt.
Ex qua ſpeculatione, oritur regula ab antiquis tradita
inueniendi vltimi numeri diſparis concurrentis ad compo
ſitionem
ſitionem alicuius quadrati. Vt ſi quis ſeire deſideret nu-
merum vltimum diſparem, quo mediante quadratum .
o.n. conſtitutum fuit, quod aliud non eſt quam ſcire
quantus ſit numerus vltimi gnomonis .i.n.a. æqualis gno
moni .i.o.a. Itaque vt ſciamus hunc gnomonem .i.o.a.
patet duplicandam eſſe radicem .o.e.b.i. dabiturque, .o.e.
b.i. et .o.u.d.a. vbi bis reperitur .o. nos autem tantummo
do quærimus ſcire gnomonem .i.b.e.o.u.d.a. Itaque
minor eſt vnitate duplo radicis, cum unitas .o. bis repe-
tatur, quæ tamen in gnomone ſemel tantum ſumebatur.
THEOREMA XCI.
CVR ſumma quadratorum, quorum radices ſunt in proportione ſeſquitertia
nempe .4. ad .3. quadrata ſit.
nempe .4. ad .3. quadrata ſit.
Exempli gratia, ſumemus quadratum .3. ſcilicet 9. quod in ſummam cum qua-
drato .4. colligemus, nempè .16. eritque; quadratum .25. & ita quadratum .6. hoc eſt .
36. collectum cum quadrato .8. nempè .64. efficiet quadratum .100. ita etiam qua-
dratum .9. hoceſt .81. coniunctum quadrato .12. nempè .144. producet quadra-
tum .225.
drato .4. colligemus, nempè .16. eritque; quadratum .25. & ita quadratum .6. hoc eſt .
36. collectum cum quadrato .8. nempè .64. efficiet quadratum .100. ita etiam qua-
dratum .9. hoceſt .81. coniunctum quadrato .12. nempè .144. producet quadra-
tum .225.
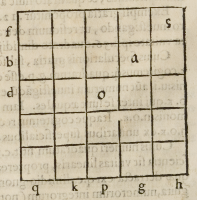
In cuius gratiam ſint duo quadrata ſubſcripta .q.o. et .q.a. quorum radices ſint .q.
 100[Figure 100]
g. et .q.p. hoc eſt .q.g. quatuor vnitatum, et .q.
100[Figure 100]
g. et .q.p. hoc eſt .q.g. quatuor vnitatum, et .q.
p. trium, ex quo .q.a. erit .16. vnitatum et .q.o.
nouem. Ad hæc cogitemus applicari quadra-
to .q.a. gnomonem .f.s.h. tam amplum ſiue la-
tum quam gnomon .b.a.g. nempè vt .h. ſit æqua
lis .g: g. verò differentia ſit qua .q.g. maior eſt .
q.p. huncque; gnomonem .f.s.h. dico ęqualem eſ
ſe quadrato .q.o. nam ex preſuppoſito .g. terra
dicem .q.p. ingreditur, & quater .q.g. ex quo,
tres partes .q.k.p. inter ſe æquales ſunt vnde
etiam quadratum .q.o. nouem partibus ſuper-
ficialibus quadratis conſtabit, quarum ſingula
rum radix æqualis erit .g. cumque præcedenti
theoremate didicerimus quemlibet gnomo-
nem quadrati immediatè ſequentis æquę amplitudinis cum gnomone præcedentis,
p. trium, ex quo .q.a. erit .16. vnitatum et .q.o.
nouem. Ad hæc cogitemus applicari quadra-
to .q.a. gnomonem .f.s.h. tam amplum ſiue la-
tum quam gnomon .b.a.g. nempè vt .h. ſit æqua
lis .g: g. verò differentia ſit qua .q.g. maior eſt .
q.p. huncque; gnomonem .f.s.h. dico ęqualem eſ
ſe quadrato .q.o. nam ex preſuppoſito .g. terra
dicem .q.p. ingreditur, & quater .q.g. ex quo,
tres partes .q.k.p. inter ſe æquales ſunt vnde
etiam quadratum .q.o. nouem partibus ſuper-
ficialibus quadratis conſtabit, quarum ſingula
rum radix æqualis erit .g. cumque præcedenti
theoremate didicerimus quemlibet gnomo-
nem quadrati immediatè ſequentis æquę amplitudinis cum gnomone præcedentis,

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib