7361THEOR. ARITH.
n.k. ipſius quadratum numerorum integrorum cognoſcetur, cui addito gnomone .
n.o.K. cognoſcemus numerum .u.i. quæſitum.
n.o.K. cognoſcemus numerum .u.i. quæſitum.
Sed cum nobis hæc via, tenenda propoſitum non fuit, hoc eſt primo loco inue
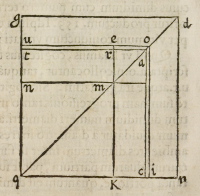
niendi quadrati minoris .n.K. ideo ſupereſt probandum gnomonem .t.o.c. vnitati ae-
qualem eſſe, nempe quadratulo .m.a. quod patebit, ſi conſideremus nos ſumpſiſſe
rectangulum .r.c. pro dimidio gnomonis .n.o.K. etenim ſi ſupplemento etiam .n.r. qua
dratulum æquale .m.a. adderetur, pateret gnomonem .n.a.K. cum dicto quadratulo
collectum, æqualem eſſe gnomoni .n.o.K: cum duo ſupplementa .m.t. et .m.c. inter ſe
fint æqualia. Quamobrem inuento quadrato .t.c. ex dimidio gnomonis cognito,
additur vnitas, gnomon ſcilicet .t.o.c. ex quo cognoſcitur numerus .u.i. quæſitus.
Quod autem quadratum .g.p. numeris integris conſtet, hac ratione probatur viſum
enim fuit ſupra quadratum .n.K. verè quadratum eſſe, & numeris integris conſtare,
pariter etiam .t.c. ſeque; mutuo conſequi (nam .K.c. eſt vnitas linearis) ex quo gnomon
n.a.K. numero diſpari conſtabit, ex ijs quæ .90. theoremate probata fuerunt. Itaque;
ex eodem theoremate neceſſe eſt gnomonem .t.d.c. etiam numero diſpari conſtare,
ita vt à numero .n.a.K. non niſi duabus vnitatibus differat, nempe vt .c.p. ſit vnitas li-
nearis, ſed ita reuera eſt, numerus enim .u.d.i. ex præſuppoſito par eſt, quare nume
rus .t.d.c. diſpar erit, cum alterum vnitate ſuperet, videlicet gnomone .t.o.c. vnita
ri æquali, tum .n.a.K. minor eſt .n.o.K. ex eodem gnomone .t.o.c. unitati æquali. Ita
que .n.a.K. minor erit .u.d.i. per vnitatem, & minor .t.d.c. per duas unitates, ex quo ſe-
quitur .g.p. eſſe quadratum integrorum ex dicto theoremate ac con ſequens quadrato
t.c. quare .c.p. vnitas erit, & radices .q.K. et .q.p. horum quadratorum numero bina-
rio inter ſe different. Vnà etiam ſcienda eſt cauſa, cur numerus propoſitus neceſſa
 102[Figure 102]
riò binario maior eſſe debeat.
Etenim cum ipſe
102[Figure 102]
riò binario maior eſſe debeat.
Etenim cum ipſe
ſit futurus gnomon .n.o.K. nec poſſit minor eſſe
numero ternario, vt patet ex .90. theoremate,
idcirco ſequitur neceſſariò maiorem eſſe bina-
rio debere. Quòd ſi diſpar numerus propone-
retur, nec forma operis nec ſpeculationis mutan-
da eſſet. Non erit tamen neceſſarium vt ipſa
quadrata .n.K. et .g.p. numeris integris conſta-
rent. Sæpius enim fractis componerentur, quod
ex .90. theoremate facile erit ſpeculari nihilo-
minus fractis integris, ipſisque; collectis cum ſuis
fractis ſummæ eſſent quadratæ.
niendi quadrati minoris .n.K. ideo ſupereſt probandum gnomonem .t.o.c. vnitati ae-
qualem eſſe, nempe quadratulo .m.a. quod patebit, ſi conſideremus nos ſumpſiſſe
rectangulum .r.c. pro dimidio gnomonis .n.o.K. etenim ſi ſupplemento etiam .n.r. qua
dratulum æquale .m.a. adderetur, pateret gnomonem .n.a.K. cum dicto quadratulo
collectum, æqualem eſſe gnomoni .n.o.K: cum duo ſupplementa .m.t. et .m.c. inter ſe
fint æqualia. Quamobrem inuento quadrato .t.c. ex dimidio gnomonis cognito,
additur vnitas, gnomon ſcilicet .t.o.c. ex quo cognoſcitur numerus .u.i. quæſitus.
Quod autem quadratum .g.p. numeris integris conſtet, hac ratione probatur viſum
enim fuit ſupra quadratum .n.K. verè quadratum eſſe, & numeris integris conſtare,
pariter etiam .t.c. ſeque; mutuo conſequi (nam .K.c. eſt vnitas linearis) ex quo gnomon
n.a.K. numero diſpari conſtabit, ex ijs quæ .90. theoremate probata fuerunt. Itaque;
ex eodem theoremate neceſſe eſt gnomonem .t.d.c. etiam numero diſpari conſtare,
ita vt à numero .n.a.K. non niſi duabus vnitatibus differat, nempe vt .c.p. ſit vnitas li-
nearis, ſed ita reuera eſt, numerus enim .u.d.i. ex præſuppoſito par eſt, quare nume
rus .t.d.c. diſpar erit, cum alterum vnitate ſuperet, videlicet gnomone .t.o.c. vnita
ri æquali, tum .n.a.K. minor eſt .n.o.K. ex eodem gnomone .t.o.c. unitati æquali. Ita
que .n.a.K. minor erit .u.d.i. per vnitatem, & minor .t.d.c. per duas unitates, ex quo ſe-
quitur .g.p. eſſe quadratum integrorum ex dicto theoremate ac con ſequens quadrato
t.c. quare .c.p. vnitas erit, & radices .q.K. et .q.p. horum quadratorum numero bina-
rio inter ſe different. Vnà etiam ſcienda eſt cauſa, cur numerus propoſitus neceſſa
ſit futurus gnomon .n.o.K. nec poſſit minor eſſe
numero ternario, vt patet ex .90. theoremate,
idcirco ſequitur neceſſariò maiorem eſſe bina-
rio debere. Quòd ſi diſpar numerus propone-
retur, nec forma operis nec ſpeculationis mutan-
da eſſet. Non erit tamen neceſſarium vt ipſa
quadrata .n.K. et .g.p. numeris integris conſta-
rent. Sæpius enim fractis componerentur, quod
ex .90. theoremate facile erit ſpeculari nihilo-
minus fractis integris, ipſisque; collectis cum ſuis
fractis ſummæ eſſent quadratæ.
THEOREMA XCIII.
CVR propoſitis duobus numeris altero pari, altero verò diſpari, duplo primi
minore per vnitatem, ſi alium inuenire numerum voluerimus, cui alterum iſto
rum coniunctum proferat quadratum, & altero detracto, quadratum ſuperſit. Re-
ctè datos numeros in ſummam colligemus, quam ſummam in duas quam maximas
poterimus partes diuidemus, quarum vna pari, altera diſpari conſtet, tum vtran-
que in ſeipſam multiplicabimus, & quadrato minori, duorum numerorum propo-
ſitorum quemuis ademus, ex quo cupimus nobis quadratum minus ſupereſſe, & pro
ueniet nobis numerum quæſitum.
minore per vnitatem, ſi alium inuenire numerum voluerimus, cui alterum iſto
rum coniunctum proferat quadratum, & altero detracto, quadratum ſuperſit. Re-
ctè datos numeros in ſummam colligemus, quam ſummam in duas quam maximas
poterimus partes diuidemus, quarum vna pari, altera diſpari conſtet, tum vtran-
que in ſeipſam multiplicabimus, & quadrato minori, duorum numerorum propo-
ſitorum quemuis ademus, ex quo cupimus nobis quadratum minus ſupereſſe, & pro
ueniet nobis numerum quæſitum.
Exempli gtatia, proponuntur numeri .11. et .6. quorum alter alicui numero ad-

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib