357345EPISTOL AE.
puncti .l. clarum igitur nunc habes, quod in ſphærico concauo, ſeu conuexo, non
omnes radij reflexi conueniunt in vno, eodemque; puncto catheti incidentiæ, quemad
modum in planis accidit, in quibus ſemper vnum, & idem punctum eſt ipſis commu
ne in ipſo incidentiæ catheto.
omnes radij reflexi conueniunt in vno, eodemque; puncto catheti incidentiæ, quemad
modum in planis accidit, in quibus ſemper vnum, & idem punctum eſt ipſis commu
ne in ipſo incidentiæ catheto.
Non prætermittam etiam hunc alium breuiorem modum ſpeculandi æqualita-
tem depreſſionis imaginis ſub ſpeculo plano, ei quæ ſupra reperitur ipſius obiecti, in ca
theto incidentiæ, quemadmodum nu nc
vltimò diximus, hoc eſt quod cum
 389[Figure 389]
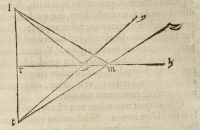
imago obiecti .l. reflexa à puncto .
389[Figure 389]
imago obiecti .l. reflexa à puncto .
x. reperiatur in linea .y.x.t. & ima-
go eiuſdem obiecti reflexa à pun-
cto .m. reperiatur in linea .z.m.t. &
iſtæ duæ lineę ſeinuicem ſecent in
puncto .t. ipſius catheti, exiſtente .
r.t. æquali .r.l. vt nunc vidimus, er-
go ſemper imago reflexa à ſpecu-
lo plano, nobis apparebit in ipſo ca
theto, tam vltra ſpeculum, quam ci
tra ipſum, repertum fuerit ipsum obiectum
quod nec Alhazem, nec Vitellio,
nec alius aliquis (quod ſciam) ad huc ſcientificè demonſtrauit. exempla enim vel ex
perientia non faciunt ſcire. Credo etiam te non dubitare quin duæ lineæ .y.x. et .z.
m. inuicem concurrant, cum anguli .t.x.m. et .t.m.x. minores ſint duobus rectis cum
æquales ſint angulis .l.x.m. et .l.m.x.
tem depreſſionis imaginis ſub ſpeculo plano, ei quæ ſupra reperitur ipſius obiecti, in ca
theto incidentiæ, quemadmodum nu nc
vltimò diximus, hoc eſt quod cum
x. reperiatur in linea .y.x.t. & ima-
go eiuſdem obiecti reflexa à pun-
cto .m. reperiatur in linea .z.m.t. &
iſtæ duæ lineę ſeinuicem ſecent in
puncto .t. ipſius catheti, exiſtente .
r.t. æquali .r.l. vt nunc vidimus, er-
go ſemper imago reflexa à ſpecu-
lo plano, nobis apparebit in ipſo ca
theto, tam vltra ſpeculum, quam ci
tra ipſum, repertum fuerit ipsum obiectum
quod nec Alhazem, nec Vitellio,
nec alius aliquis (quod ſciam) ad huc ſcientificè demonſtrauit. exempla enim vel ex
perientia non faciunt ſcire. Credo etiam te non dubitare quin duæ lineæ .y.x. et .z.
m. inuicem concurrant, cum anguli .t.x.m. et .t.m.x. minores ſint duobus rectis cum
æquales ſint angulis .l.x.m. et .l.m.x.
De rotunditate vmbræterræ in ecclipſibus Lunaribus.
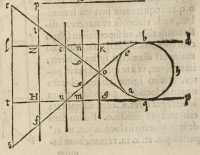
ROtunditas vmbræ in ecclipſi-
 390[Figure 390]
bus lunaribus oritur tam à rotun
390[Figure 390]
bus lunaribus oritur tam à rotun
ditate maris, quam terræ, & ſi terra eſ-
ſet etiam cuiuſuis alterius figurę, quam
ſphæricę, dummodo aqua impleret
locum ſphęriceitatis à terra derelictum,
nihilominus vmbra eſſet rotunda,
quę quidem ab aqua produceretur,
quanuis Alexander Piccolhomineus
 391[Figure 391]
aliter ſentiat in libro de magnitudi-
391[Figure 391]
aliter ſentiat in libro de magnitudi-
ne terrę, & aquæ.
ditate maris, quam terræ, & ſi terra eſ-
ſet etiam cuiuſuis alterius figurę, quam
ſphæricę, dummodo aqua impleret
locum ſphęriceitatis à terra derelictum,
nihilominus vmbra eſſet rotunda,
quę quidem ab aqua produceretur,
quanuis Alexander Piccolhomineus
ne terrę, & aquæ.
Sciendum enim eſt, quod omne cor
pus in ſe habens aliquantulum opaci-
tatis, ſemper debilitat radium lumino
ſum, & tanto magis, quanto magis in ip
ſo corpore radius penetrat, etiam & ſi
ad rectos incideret ipſe radius ſupra
ſuperficiem ipſius corporis. Exempli gra
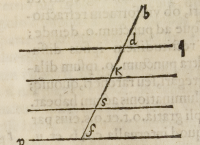
tia, eſto .q.p. corpus a queum, cuius pro
funditas diuidatur in partibus .d.K:
K.s: et .s.f. à puncto verò lucido .b.
pus in ſe habens aliquantulum opaci-
tatis, ſemper debilitat radium lumino
ſum, & tanto magis, quanto magis in ip
ſo corpore radius penetrat, etiam & ſi
ad rectos incideret ipſe radius ſupra
ſuperficiem ipſius corporis. Exempli gra
tia, eſto .q.p. corpus a queum, cuius pro
funditas diuidatur in partibus .d.K:
K.s: et .s.f. à puncto verò lucido .b.
