4735THEOREM. ARIT.
Sumantur enimtres numeri continui proportionales, cuiuſcunque denique pro
portionalitatis, qui in ſummam colligantur, ac poſtmodum, regula de trib. dica-
mus. Si ſumma hæc primo numero propoſito in tres partes diuidendo reſpondet,
cuireſpondebit vna ex tribus partibus huiuſcę summæ? idem dereliquis duabus parti
bus dico.
portionalitatis, qui in ſummam colligantur, ac poſtmodum, regula de trib. dica-
mus. Si ſumma hæc primo numero propoſito in tres partes diuidendo reſpondet,
cuireſpondebit vna ex tribus partibus huiuſcę summæ? idem dereliquis duabus parti
bus dico.
Exempli gratia, ſi proponatur numerus .57. diuidendus in tres continuas partes
proportionales proportione ſeſquialtera, tres numeros in eiuſmodi proportio-
nalitate diſtinctos ſumemus, vt potè .4. 6. 9. qui in ſummam collecti dabunt ſum-
mam .19. dicemusque; ſi .19. dant .4. quid dabunt .57? vnde proueniens vnius partis erit .
12. Tum ſi dicamus, ſi .19. dat .6. quid dabit .57? nempe dabit .18. Poſtremò, ſi .
19. dat .9. quid dabit .57? nempe .26. atque ita dabitur .18. cuius quadratum æqua-
bitur producto reliquarum duarum partium inter ſe.
proportionales proportione ſeſquialtera, tres numeros in eiuſmodi proportio-
nalitate diſtinctos ſumemus, vt potè .4. 6. 9. qui in ſummam collecti dabunt ſum-
mam .19. dicemusque; ſi .19. dant .4. quid dabunt .57? vnde proueniens vnius partis erit .
12. Tum ſi dicamus, ſi .19. dat .6. quid dabit .57? nempe dabit .18. Poſtremò, ſi .
19. dat .9. quid dabit .57? nempe .26. atque ita dabitur .18. cuius quadratum æqua-
bitur producto reliquarum duarum partium inter ſe.
Quod vt ſciamus, numerus propoſitus in tres quaſlibet partes diuidendus ſi-
gnificetur linea .a.d. tres autem numeri dictæ proportionalitatis, lineis .e.f: f.g.
et .g.h. directè inter ſe coniunctis denotentur. Cogitemus pariter lineam .d.a. in
tres partes diuiſam .a.b: b.c. et .c.d. eadem cum cæteris proportionalitate, tunc ea-
dem erit proportio .a.d. ad quamlibet ſuarum partium, quæ eſt .e.h. ad reſponden
tem ipſius in .a.d: Verbi gratia reſpondentem .a.b. ipſi .e.f. et .b.c: f.g. et .c.d: g.h. Di
co enim quòd ita ſe habebit .a.d. ad .c.d. ſicut .e.h. ad .g.h. Nam cum ſic ſe habeat .a.
b. ad .b.c. ſicut .e.f. ad .f.g. ex præſuppoſito, permutando ſic ſe habebit .a.b. ad .e.f. ſi-
cut .b.c. ad .f.g. & eadem ratione ſic ſe habe-
bit .c.d. ad .g.h. ſicut .b.c. ad .f.g. & conſequen-
ter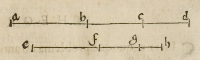 64[Figure 64]
conſequen-
64[Figure 64]
conſequen-
ter ſicut .a.b. ad .e.f. ex quo ex .13. quinti ſic
ſe habebit tota .a.d. ad totam .e.h. ſicut .c.d.
ad .g.h. aut .b.c. ad .f.g. aut .a.b. ad .e.f. per-
mutando itaque propoſitum manifeſtum erit, ipſum autem productum .a.b. in .c.b.
æquale erit quadrato .b.c. ex .15. fexti aut .20. ſeptimi.
gnificetur linea .a.d. tres autem numeri dictæ proportionalitatis, lineis .e.f: f.g.
et .g.h. directè inter ſe coniunctis denotentur. Cogitemus pariter lineam .d.a. in
tres partes diuiſam .a.b: b.c. et .c.d. eadem cum cæteris proportionalitate, tunc ea-
dem erit proportio .a.d. ad quamlibet ſuarum partium, quæ eſt .e.h. ad reſponden
tem ipſius in .a.d: Verbi gratia reſpondentem .a.b. ipſi .e.f. et .b.c: f.g. et .c.d: g.h. Di
co enim quòd ita ſe habebit .a.d. ad .c.d. ſicut .e.h. ad .g.h. Nam cum ſic ſe habeat .a.
b. ad .b.c. ſicut .e.f. ad .f.g. ex præſuppoſito, permutando ſic ſe habebit .a.b. ad .e.f. ſi-
cut .b.c. ad .f.g. & eadem ratione ſic ſe habe-
bit .c.d. ad .g.h. ſicut .b.c. ad .f.g. & conſequen-
ter
ter ſicut .a.b. ad .e.f. ex quo ex .13. quinti ſic
ſe habebit tota .a.d. ad totam .e.h. ſicut .c.d.
ad .g.h. aut .b.c. ad .f.g. aut .a.b. ad .e.f. per-
mutando itaque propoſitum manifeſtum erit, ipſum autem productum .a.b. in .c.b.
æquale erit quadrato .b.c. ex .15. fexti aut .20. ſeptimi.
THEOREMA LVI.
VEteres aliud quoque problema indeterminatum propoſuerunt, quod ex
more ratione à me definietur, eſt autem eiuſmodi.
more ratione à me definietur, eſt autem eiuſmodi.
Quomodo propoſitus numerus in tres eiuſmodi partes diuidatur, vt quadratum
vnius æquale fit fummæ quadratorum reliquarum duarum partium.
vnius æquale fit fummæ quadratorum reliquarum duarum partium.
Hoc vt efficiamus tria quadrata ſeparata ſumamus, quorum vnum æquale ſit reliquis
duobus; eorum autem radices in ſummam ſimul colligantur, tum regulam de tribus ſe
quemur, ratione præcedenti theoremate demonſtrata, & rectè vt infra docebimus,
quod autem dico de quadratis, etiam de cubis, & quibuſuis dignitatibus aſſero.
duobus; eorum autem radices in ſummam ſimul colligantur, tum regulam de tribus ſe
quemur, ratione præcedenti theoremate demonſtrata, & rectè vt infra docebimus,
quod autem dico de quadratis, etiam de cubis, & quibuſuis dignitatibus aſſero.
Exempli gratia, ſi numerus diuiſibilis proponatur .30. in tres eiuſmodi partes di
uidendus, vt quadratum vnius æquale ſit ſummæ quadratorum reliquarum duarum
partium, in primis radices trium quadratorum ſumemus, ſic quomodocunque ſe
habentes, vt maius ipſorum æquale ſit ſummæ reliquorum duorum, verbi gratia .25.
16. et .9. nempe .5. 4. et .3. quæ ſi colligantur in ſummam efficiunt .12. Tum ex regu-
la de tribus dicemus, ſi .12. reſpondet .30: cui, 5. radix maior reſpondebit? nem-
pe .12. cum dimidio.
uidendus, vt quadratum vnius æquale ſit ſummæ quadratorum reliquarum duarum
partium, in primis radices trium quadratorum ſumemus, ſic quomodocunque ſe
habentes, vt maius ipſorum æquale ſit ſummæ reliquorum duorum, verbi gratia .25.
16. et .9. nempe .5. 4. et .3. quæ ſi colligantur in ſummam efficiunt .12. Tum ex regu-
la de tribus dicemus, ſi .12. reſpondet .30: cui, 5. radix maior reſpondebit? nem-
pe .12. cum dimidio.
Deinde ſi dixerimus ſi .12. valet .30. quid valebit .4. radix media?
nempe vale-
bit .10. tertia autem minor .7. cum dimidio. Itaquetota ſumma erit .30. & quadra-
bit .10. tertia autem minor .7. cum dimidio. Itaquetota ſumma erit .30. & quadra-
