8573THEOREM. ARITH.
nis, ex quo .m.k. prolixior erit .e.d. ex præſup poſito.
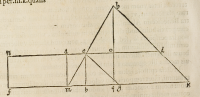
Poſtmodum .m.e. et .k.d. dua-
bus lineis rectis coniungantur, quæ productæ concurrentin puncto .b. ducatur pari-
ter .e.g. à puncto .e. parallela .b.k. et .m.a: e.h. et .b.q. parallelæ .f.n. ex quo .f.m. æqua-
lis erit .n.a. et .m.h: a.e. et .h.q: e.o. et .g.k: e.d. et .f.q: n.o. ex .34. primi Eucli. vnde pro
portio .m.h. ad .h.q. erit vt .m.g. ad .g.k. quandoquidem vtraque æqualis eſt propor-
tioni .m.e. ad .e.b. ex .2. ſexti, ſed cum .m.k. et .g.k. notæ ſint, pariter cognoſcetur .m.
g. ſecundum reſiduum, cum etiam notæ ſint .n.e. et .n.a. Itaque cognoſcemus .a.e. hoc
eſt .m.h. cognitis verò .m.g: g.k. et .m.h. ex .15. ſexti aut .20. ſeptimi cognoſcetur .h.
q. erit igitur .a.e. aut quod idem eſt .m. hprimum reſiduum, et .m.g. ſecundum, et .h.
q. aut .e.o. proueniens, et .n.o. et .f.q. itinera vtriuſque viatoris inter ſe æqualia.
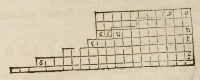
Nec verò prætermittenda eſt ſpeculatio vltimæ rationis inueniendæ quantitatis
diei, quæ conſtat ope diuiſionis producti .m.h. in .24. per .m.g. Ea autem eiuſmodi
eſt. Probatum fuit ſic ſe habere .m.h. ad .h.q. ut .m.g. ad .g.k. Itaque componendo
ſic ſe habebit .m.q. ad .h.q. vt .m.k. ad .g.k. & permutando .m.q. ad .m.k. vt .h.q. ad .g.
k. Sed cum ſic ſe habeat .m.h. ad .h.q. vt .m.g. ad .g.k. permutando ſic ſe habebit .m.
h. ad .m.g. vt .h.q. ad .g.k. itaque
ex .11. quinti ita .m.h. ad .m.g. vt .
 116[Figure 116]
m.q. ad .m.k. ex quo permutando
116[Figure 116]
m.q. ad .m.k. ex quo permutando
m.h. ad .m.q. vt .m.g. ad .m.k. ſed
cum .m.k. ſit motus toti diei reſpon
dens, ſecurè dicere poterimus, ſi
m.g. talis eſt reſpectu horarum .
24. ſignificatarum per .m.k. qualis
 117[Figure 117]
erit .m.h. & quo
117[Figure 117]
erit .m.h. & quo
tæ parti dieire-
ſpondens: quæ
poſtmodum erit .
m.q. quæ, vt di-
ctum fuit, talis eſt
reſpectu .m.k.
qualis .m.h. re-
ſpectu .m.g. Reli
quę duæ ſpecula
tiones priorum
modorum, vna &
eadem eſt, facilisque; per ſe mediocriter intelligenti. Eodem modo reliquæ omnes
progreſſiones ſecundi viatoris cum rectangulo primi conferri ex hoc theoremate
poterunt.
bus lineis rectis coniungantur, quæ productæ concurrentin puncto .b. ducatur pari-
ter .e.g. à puncto .e. parallela .b.k. et .m.a: e.h. et .b.q. parallelæ .f.n. ex quo .f.m. æqua-
lis erit .n.a. et .m.h: a.e. et .h.q: e.o. et .g.k: e.d. et .f.q: n.o. ex .34. primi Eucli. vnde pro
portio .m.h. ad .h.q. erit vt .m.g. ad .g.k. quandoquidem vtraque æqualis eſt propor-
tioni .m.e. ad .e.b. ex .2. ſexti, ſed cum .m.k. et .g.k. notæ ſint, pariter cognoſcetur .m.
g. ſecundum reſiduum, cum etiam notæ ſint .n.e. et .n.a. Itaque cognoſcemus .a.e. hoc
eſt .m.h. cognitis verò .m.g: g.k. et .m.h. ex .15. ſexti aut .20. ſeptimi cognoſcetur .h.
q. erit igitur .a.e. aut quod idem eſt .m. hprimum reſiduum, et .m.g. ſecundum, et .h.
q. aut .e.o. proueniens, et .n.o. et .f.q. itinera vtriuſque viatoris inter ſe æqualia.
Nec verò prætermittenda eſt ſpeculatio vltimæ rationis inueniendæ quantitatis
diei, quæ conſtat ope diuiſionis producti .m.h. in .24. per .m.g. Ea autem eiuſmodi
eſt. Probatum fuit ſic ſe habere .m.h. ad .h.q. ut .m.g. ad .g.k. Itaque componendo
ſic ſe habebit .m.q. ad .h.q. vt .m.k. ad .g.k. & permutando .m.q. ad .m.k. vt .h.q. ad .g.
k. Sed cum ſic ſe habeat .m.h. ad .h.q. vt .m.g. ad .g.k. permutando ſic ſe habebit .m.
h. ad .m.g. vt .h.q. ad .g.k. itaque
ex .11. quinti ita .m.h. ad .m.g. vt .
m.h. ad .m.q. vt .m.g. ad .m.k. ſed
cum .m.k. ſit motus toti diei reſpon
dens, ſecurè dicere poterimus, ſi
m.g. talis eſt reſpectu horarum .
24. ſignificatarum per .m.k. qualis
tæ parti dieire-
ſpondens: quæ
poſtmodum erit .
m.q. quæ, vt di-
ctum fuit, talis eſt
reſpectu .m.k.
qualis .m.h. re-
ſpectu .m.g. Reli
quę duæ ſpecula
tiones priorum
modorum, vna &
eadem eſt, facilisque; per ſe mediocriter intelligenti. Eodem modo reliquæ omnes
progreſſiones ſecundi viatoris cum rectangulo primi conferri ex hoc theoremate
poterunt.
THEOREMA CXIII.
PRoponitur & aliud, primum ſcilicet viatorem iter incipere diebus aliquot an-
tè ſecundum, primum tamen lentius, quàm ſecundum ambulare, & utrunque
eorum certa quædam milliaria conficere. Iam ſiſcire voluerimus in quot diebus
ſeſe conſequentur, uulgaris regula iubet, inſpici quot milliaria primus ſolus iter a-
gens confecerit, tum animaduerti differentiam diurnam motus vnius ab altero, atque;
milliarium numerum primi viatoris ſoli abundantis per hanc differentiam diuidi, pro
ueniens autem erit numerus dierum quæſitus.
tè ſecundum, primum tamen lentius, quàm ſecundum ambulare, & utrunque
eorum certa quædam milliaria conficere. Iam ſiſcire voluerimus in quot diebus
ſeſe conſequentur, uulgaris regula iubet, inſpici quot milliaria primus ſolus iter a-
gens confecerit, tum animaduerti differentiam diurnam motus vnius ab altero, atque;
milliarium numerum primi viatoris ſoli abundantis per hanc differentiam diuidi, pro
ueniens autem erit numerus dierum quæſitus.
