5846IO. BAPT. BENED.
g.m. cogiteturque; rectangulum .y.x. & rectangulum .k.x.
Itaque dabitur eadem pro
portio .k.m. ad .m.x. nempe .k.x. rectanguli ad .m.g. quæ eſt .b.a. ad .o.e. et .y.x. ad .m.
g. quæ .b.a. ad .a.o. ſed ex prima ſexti aut .18. vel .19. ſeptimi, ſic ſe habet rectangu-
lum .k.y. ad .x.y. ſicut .k.m. ad .m.x. quare ſicut .b.a. ad .o.e. ex .11. quinti, & eiuſdem
rectanguli .k.y. ad rectangulum .k.x. ſicut .y.m. ad .x.m. nempe .b.a. ad .a.o. Quare
ex communi ſcientia, ſic ſe habebit duplum rectanguli .k.y. ad ſummam .y.x. cum .
k.x. rectangulorum, ſicut duplum .b.a. ad ſummam .a.o.e. et proportio ſummæ re-
ctangulorum .y.x. et .k.x. duplo .g.m. ſicut duplum .b.a. ad .a.o.e. Igitur ſumma duo-
rum rectangulorum .y.x. et .x.k. media proportionalis erit inter duplum rectanguli .
k.y. & duplum vnitatis ſuperſicialis .g.m. Nunc terminetur rectangulum .a.r. ex quo
dabitur eadem proportio dupli .a.s. ad .a.r. ſicut dupli .b.a. ad .a.e. ex propoſitioni-
bus notatis, ſexti aut ſeptimi. Quare etiam ſicut dupli rectanguli .k.y. ad ſummam
rectangulorum .y.x. et .k.x. Iam verò ſi conſtituatur .e.c. pro vnitate lineari ipſius .
e.r. certi erimus numerum .a.c. æqualem eſſe .a.e. & proportionem .r.e. ad .e.c. hoc
eſt .a.r. ad .a.c. eandem quæ .y.x. et .x.k. rectangulorum ad .m.g. ex prædictis rationi-
bus, & ex hypotheſi, nempe quòd .
e.r. æqualis ſit numero .k.m.y.
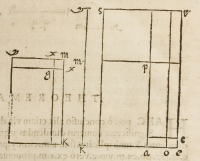 79[Figure 79]
hoc eſt rectangulorum .y.x. et .x.
79[Figure 79]
hoc eſt rectangulorum .y.x. et .x.
k. Quamobrem .a.r. ex communi
ſcientia medium proportionale erit
inter duplum .a.s. & duplum .a.c. ea
demque; proportio dupli prędicti .a.s. ad
duplum .a.c. ex æqualitate propor-
tionum ſimul collectarum, eadem
erit qùæ proportio dupli rectangu-
li .k.y. ad duplum .m.g. hoc eſt .a.s.
ſimplicis ad ſimplicem .a.c. quæ ſim
plicis rectanguli .k.y. ad ſimplicem
vnitatem .g.m. ſic enim ſe habet ſim
plex ad ſimplex, ſicut duplum ad
duplum. Sed pariter ita ſe habet .a.s. ad .a. c. cogitato .a.c. tamquam proueniente
ex diuiſione .a.s. per rectangulum .k.y. vt conſtitutum eſt, ſicut .k.y. ad .m.g. ex defi-
nitione diuiſionis vt iam dictum eſt, quare numerus .a.c. æqualis erit numero .a.o.e.
portio .k.m. ad .m.x. nempe .k.x. rectanguli ad .m.g. quæ eſt .b.a. ad .o.e. et .y.x. ad .m.
g. quæ .b.a. ad .a.o. ſed ex prima ſexti aut .18. vel .19. ſeptimi, ſic ſe habet rectangu-
lum .k.y. ad .x.y. ſicut .k.m. ad .m.x. quare ſicut .b.a. ad .o.e. ex .11. quinti, & eiuſdem
rectanguli .k.y. ad rectangulum .k.x. ſicut .y.m. ad .x.m. nempe .b.a. ad .a.o. Quare
ex communi ſcientia, ſic ſe habebit duplum rectanguli .k.y. ad ſummam .y.x. cum .
k.x. rectangulorum, ſicut duplum .b.a. ad ſummam .a.o.e. et proportio ſummæ re-
ctangulorum .y.x. et .k.x. duplo .g.m. ſicut duplum .b.a. ad .a.o.e. Igitur ſumma duo-
rum rectangulorum .y.x. et .x.k. media proportionalis erit inter duplum rectanguli .
k.y. & duplum vnitatis ſuperſicialis .g.m. Nunc terminetur rectangulum .a.r. ex quo
dabitur eadem proportio dupli .a.s. ad .a.r. ſicut dupli .b.a. ad .a.e. ex propoſitioni-
bus notatis, ſexti aut ſeptimi. Quare etiam ſicut dupli rectanguli .k.y. ad ſummam
rectangulorum .y.x. et .k.x. Iam verò ſi conſtituatur .e.c. pro vnitate lineari ipſius .
e.r. certi erimus numerum .a.c. æqualem eſſe .a.e. & proportionem .r.e. ad .e.c. hoc
eſt .a.r. ad .a.c. eandem quæ .y.x. et .x.k. rectangulorum ad .m.g. ex prædictis rationi-
bus, & ex hypotheſi, nempe quòd .
e.r. æqualis ſit numero .k.m.y.
k. Quamobrem .a.r. ex communi
ſcientia medium proportionale erit
inter duplum .a.s. & duplum .a.c. ea
demque; proportio dupli prędicti .a.s. ad
duplum .a.c. ex æqualitate propor-
tionum ſimul collectarum, eadem
erit qùæ proportio dupli rectangu-
li .k.y. ad duplum .m.g. hoc eſt .a.s.
ſimplicis ad ſimplicem .a.c. quæ ſim
plicis rectanguli .k.y. ad ſimplicem
vnitatem .g.m. ſic enim ſe habet ſim
plex ad ſimplex, ſicut duplum ad
duplum. Sed pariter ita ſe habet .a.s. ad .a. c. cogitato .a.c. tamquam proueniente
ex diuiſione .a.s. per rectangulum .k.y. vt conſtitutum eſt, ſicut .k.y. ad .m.g. ex defi-
nitione diuiſionis vt iam dictum eſt, quare numerus .a.c. æqualis erit numero .a.o.e.
THEOREMA LXXI.
CVR propoſitis .4. numeris, duobus nempe diuidentibus ac duobus diuiden-
dis, ſi adinuicem diuiſi fuerint, duoque; prouenientia inuicem multiplicata quenuis nu
merum producant, qui ſeruetur, ſi deinde ijdem numeri verſa vice mutuo diuiſi fue
rint, & inter ſe multiplicata prouenientia, productum hoc, primo ſeruato numero
æquale erit.
dis, ſi adinuicem diuiſi fuerint, duoque; prouenientia inuicem multiplicata quenuis nu
merum producant, qui ſeruetur, ſi deinde ijdem numeri verſa vice mutuo diuiſi fue
rint, & inter ſe multiplicata prouenientia, productum hoc, primo ſeruato numero
æquale erit.
Exempli gratia propoſitis his .4. numeris .20. 30. 5. 10. duo autem .20. ſcilicet
et .30. ſint numeri diuidendi, porrò .5. et .10. numeri diuidentes, nempe vt primo .20
per .5. diuidatur, tum .30. per .10. producetur .4. et .3. qui ſimul multiplicati proferent .
12. tum .20. per .10. d iuiſo et .30. per .5. prouenientia erunt .2. 6. quæ inter ſe multi-
plicata producent etiam .12.
et .30. ſint numeri diuidendi, porrò .5. et .10. numeri diuidentes, nempe vt primo .20
per .5. diuidatur, tum .30. per .10. producetur .4. et .3. qui ſimul multiplicati proferent .
12. tum .20. per .10. d iuiſo et .30. per .5. prouenientia erunt .2. 6. quæ inter ſe multi-
plicata producent etiam .12.

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib