8070IO. BAPT. BENED.
g. & permutando .o.r. ad .f.o. hoc eſt ad .m.s. vt .h. ad .g. hoc eſt .y.
Quamobrem ea-
dem erit proportio .o.r. ad .m.s. quæ .n.u. ad .n.x. Abfoluantur itaque duo rectangu
la .x.i. et .u.z. ita tamen vt rectangulum .u.z. cogitetur ęquale rectangulo .x.i. cuius .x.i.
ſuperficialis numerus ex communi conceptione lineari .n.i. æqualis erit, quare ex
eadem communi conceptione, numerus ſuperficialis .u.z. lineari .n.i. æqualis erit, qui
quidem numerus in figura rectangu-
la ſuperficialis cognitandus erit, cum
 108[Figure 108]
diuidendus ſit per .h. hoc eſt per .n.u.
108[Figure 108]
diuidendus ſit per .h. hoc eſt per .n.u.
ex quo proueniens ex huiuſmodi di
uiſione erit numerus .n.z. ex ijs
quæ .10. theoremate dicta fuerunt.
Sed ex .15. fexti aut .20. ſepti-
mi eadem eſt proportio .n.i. ad .n.z.
quæ .n.u. ad .n.x. hoc eſt .o.r. ad .m.s.
videlicet vt .n.i. ad aggregatum reli-
quorum omnium terminorum .c.a: f.
r: m.s. ex præcedenti theoremate, & ex .11. quinti Euclidis. Itaque ex .9. eiuf-
dem numerus .n.z. æqualis erit ſummæ trium terminorum .c.a: f. num .s. cui coniuncto
quarto termino .b.i. propoſitum obtinetur.
dem erit proportio .o.r. ad .m.s. quæ .n.u. ad .n.x. Abfoluantur itaque duo rectangu
la .x.i. et .u.z. ita tamen vt rectangulum .u.z. cogitetur ęquale rectangulo .x.i. cuius .x.i.
ſuperficialis numerus ex communi conceptione lineari .n.i. æqualis erit, quare ex
eadem communi conceptione, numerus ſuperficialis .u.z. lineari .n.i. æqualis erit, qui
quidem numerus in figura rectangu-
la ſuperficialis cognitandus erit, cum
ex quo proueniens ex huiuſmodi di
uiſione erit numerus .n.z. ex ijs
quæ .10. theoremate dicta fuerunt.
Sed ex .15. fexti aut .20. ſepti-
mi eadem eſt proportio .n.i. ad .n.z.
quæ .n.u. ad .n.x. hoc eſt .o.r. ad .m.s.
videlicet vt .n.i. ad aggregatum reli-
quorum omnium terminorum .c.a: f.
r: m.s. ex præcedenti theoremate, & ex .11. quinti Euclidis. Itaque ex .9. eiuf-
dem numerus .n.z. æqualis erit ſummæ trium terminorum .c.a: f. num .s. cui coniuncto
quarto termino .b.i. propoſitum obtinetur.
THEOREMA CVI.
PRopoſuere veteres quæſita nonnulla de itineribus interque; hoc vnum fuit.
Po-
namus duos iter agere per eandem viam quorum alter quatuor milliaria ſin-
gulis diebus conficiat, alter verò prima die milliare vnum, ſecunda duo, tertia tria,
atque ita ſingulis diebus milliare addit; quærimus quot dierum ſpacio ſocium con
ſequetur.
namus duos iter agere per eandem viam quorum alter quatuor milliaria ſin-
gulis diebus conficiat, alter verò prima die milliare vnum, ſecunda duo, tertia tria,
atque ita ſingulis diebus milliare addit; quærimus quot dierum ſpacio ſocium con
ſequetur.
Quamobrem numerus milliarium primi viatoris duplicatur, ſic ſunt .8. milliaria.
ex quo ſemper vnitas detrahicur, quæ in præſenti exemplo erit .7. totque; dies erunt
quibus ſocius ſocium conſequetur, & milliarium numerum æqualem abſoluerit.
ex quo ſemper vnitas detrahicur, quæ in præſenti exemplo erit .7. totque; dies erunt
quibus ſocius ſocium conſequetur, & milliarium numerum æqualem abſoluerit.
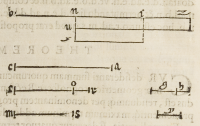
Cuius rei facilis erit ſpeculatio, ſi ſubſcripta figura diligenter conſideretur, in
qua primus viator, die prima, quatuor milliaria linea .q.d. ſignificata conficit, at-
que illa ipſa die alter vnum tantum defignatum per .d. perficit, ita vt primus via-
tor tribus milliaribus ſocium anteceſſerit, altera verò die fecundus uiator cum duo
milliaria conficiat, excedètur à primo duobus milliaribus tantummodo, quę cum tri-
bus primæ diei quinque erunt; tertia die ijſdem de cauſis primus ſex tantum millia-
ribus à ſecundo diſtabit, cum verò quarta die tot ſecundus quot primus milliaria
conficiat, primus à ſecundo amplius quam antea non diſtabit; quinta verò cum ſe
cundus vnum milliare amplius quam primus conficiat. propius accedit ad primum
vno ex ſex milliaribus, quibus anteà diſtabat, tum ſexta cum duobus primum ſupe-
ret, detrahet ex ſex milliaribus præteritæ diſtantiæ tria, ſeptima tandem illa ſex
detraxerit. In quo conſiderandum eſt ſecundum viatorem iter agere progreſſio-
ne arithmetica continua naturali .d.c.f. primum autem per rectangulum .q.f. quarum
duarum figurarum .d.o.p.f. pars communis eſſe reperitur, quæ quantitates ſi inuicem
æquales eſſe debent, neceſſe eſt ſeparatas partes .u.q.n. et .t.i.c. inter ſe æquales eſſe,
& quoniam quarta die (hoc eſt die ſic diſtante à primo, nempè numero milliarium
qua primus viator, die prima, quatuor milliaria linea .q.d. ſignificata conficit, at-
que illa ipſa die alter vnum tantum defignatum per .d. perficit, ita vt primus via-
tor tribus milliaribus ſocium anteceſſerit, altera verò die fecundus uiator cum duo
milliaria conficiat, excedètur à primo duobus milliaribus tantummodo, quę cum tri-
bus primæ diei quinque erunt; tertia die ijſdem de cauſis primus ſex tantum millia-
ribus à ſecundo diſtabit, cum verò quarta die tot ſecundus quot primus milliaria
conficiat, primus à ſecundo amplius quam antea non diſtabit; quinta verò cum ſe
cundus vnum milliare amplius quam primus conficiat. propius accedit ad primum
vno ex ſex milliaribus, quibus anteà diſtabat, tum ſexta cum duobus primum ſupe-
ret, detrahet ex ſex milliaribus præteritæ diſtantiæ tria, ſeptima tandem illa ſex
detraxerit. In quo conſiderandum eſt ſecundum viatorem iter agere progreſſio-
ne arithmetica continua naturali .d.c.f. primum autem per rectangulum .q.f. quarum
duarum figurarum .d.o.p.f. pars communis eſſe reperitur, quæ quantitates ſi inuicem
æquales eſſe debent, neceſſe eſt ſeparatas partes .u.q.n. et .t.i.c. inter ſe æquales eſſe,
& quoniam quarta die (hoc eſt die ſic diſtante à primo, nempè numero milliarium

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib