8977THEOREM. ARIT.
eo qui per .b.d. ad tempus quo .q.p. ſolum, qui per .q.p. mouetur (mo-
tus enim continui regulares & vniformes conſtituuntur) eadem ratione ita-
que ea erit proportio .q.k. ad .b.c. quæ .q.g. ad .q.p. & cum probatum
fuerit ita ſe habere .k.n. ad .c.o. vt .q.k. ad .b.c. itaque ſic ſe habebit .k.n. ad .c.
o. ut .q.g. ad .q.p. probatum etiam fuit ita ſe habere .q.k. ad .k.n. vt .b.c. ad .c.o. ex quo
componendo ſic ſe habebit .q.n. ad .n.k. vt .b.o. ad .o.c. & permutando ita .q.n. ad .b.
o. vt .k.n. ad .c.o. hoc eſt .q.g. ad .q.p. nempe vt tempus lenti ad tempus velocis itine-
rantis, & componendo ita .q.n. cum .o.b. hoc eſt .b.d. ad .b.o. vt ſumma dierum vnius &
alterius viatoris ad minorem numerum dierum velocioris. Breuiter itaque; obtineremus in
tentum quando diceremus ſi ſumma dierum, quibus iter agitur à viatoribus talis eſt (20) re-
ſpectu numeri dierum velocioris(9) qualis & cui reſpondebit totum ſpacium .b.d? vn-
de dabitur ſpacium .b.o. vnde reliqua omnia nobis cognita emergent.
tus enim continui regulares & vniformes conſtituuntur) eadem ratione ita-
que ea erit proportio .q.k. ad .b.c. quæ .q.g. ad .q.p. & cum probatum
fuerit ita ſe habere .k.n. ad .c.o. vt .q.k. ad .b.c. itaque ſic ſe habebit .k.n. ad .c.
o. ut .q.g. ad .q.p. probatum etiam fuit ita ſe habere .q.k. ad .k.n. vt .b.c. ad .c.o. ex quo
componendo ſic ſe habebit .q.n. ad .n.k. vt .b.o. ad .o.c. & permutando ita .q.n. ad .b.
o. vt .k.n. ad .c.o. hoc eſt .q.g. ad .q.p. nempe vt tempus lenti ad tempus velocis itine-
rantis, & componendo ita .q.n. cum .o.b. hoc eſt .b.d. ad .b.o. vt ſumma dierum vnius &
alterius viatoris ad minorem numerum dierum velocioris. Breuiter itaque; obtineremus in
tentum quando diceremus ſi ſumma dierum, quibus iter agitur à viatoribus talis eſt (20) re-
ſpectu numeri dierum velocioris(9) qualis & cui reſpondebit totum ſpacium .b.d? vn-
de dabitur ſpacium .b.o. vnde reliqua omnia nobis cognita emergent.
Cum autem antiquorum regula iubeat numerum dierum vnius, cum numero die-
rum alterius multiplicari, ac poſtmodum diuidi productum per ſummam omnium
dierum, rectèid quidem fit. Nam cum ſic ſe habeat .b.d. ad .b.o. vt ſumma omnium
dierum ad minorem quantitatem dierum velocioris ſcilicet. Ideo temporis propor
tio à mobili per .b.d. abſumpti ad tempus mobilis per .b.o. eadem erit, quæ ſummæ
omnium dierum ad namerum dierum velocioris. Quarerectè dicemus, ſi eiuſmodi
ſumma talem reſpectum habet ad minorem numerum dierum, quem numerum re-
ſpiciet dies ipſius .b.d? ex quo proferentur dies reſpondentes ipſi .b.o. cætera iam
dicta fuerunt.
rum alterius multiplicari, ac poſtmodum diuidi productum per ſummam omnium
dierum, rectèid quidem fit. Nam cum ſic ſe habeat .b.d. ad .b.o. vt ſumma omnium
dierum ad minorem quantitatem dierum velocioris ſcilicet. Ideo temporis propor
tio à mobili per .b.d. abſumpti ad tempus mobilis per .b.o. eadem erit, quæ ſummæ
omnium dierum ad namerum dierum velocioris. Quarerectè dicemus, ſi eiuſmodi
ſumma talem reſpectum habet ad minorem numerum dierum, quem numerum re-
ſpiciet dies ipſius .b.d? ex quo proferentur dies reſpondentes ipſi .b.o. cætera iam
dicta fuerunt.
Huiuſmodi verò ſpeculationis am-
 120[Figure 120]
plitudo ad pauciſſima verba reduci
120[Figure 120]
plitudo ad pauciſſima verba reduci
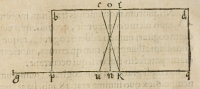
poteft, in cuius gratiam ſit ſubſcripta
figura pars inquam pręcedentis, in qua
conſtituamus .o.n. locum eum eſſe quo ſibi
viatores obuient, ex quo ſpacium .q.
n. à ſuo viatore conficietur, eo ipſo
tempore, quo à ſuo ſpacium .b.o. ita
que eadem erit proportio .q.n. ad .b.
 121[Figure 121]
o. quæ .q.g. ad .b.d. eadem erit inquam
121[Figure 121]
o. quæ .q.g. ad .b.d. eadem erit inquam
proportio .d.o. ad .o.b. quæ numeri
dierum eius, qui à .b. pergit in .d. ad
numerum dierum alterius qui à .q. in
p. proficiſcitur, & componendo eadem
erit proportio .d.b. ad .b.o. quæ ſum-
mæ dierum ad minorem numerum ipſorum, & eadem quæ dierum .b.d. ad dies
ipſius .b.o.
poteft, in cuius gratiam ſit ſubſcripta
figura pars inquam pręcedentis, in qua
conſtituamus .o.n. locum eum eſſe quo ſibi
viatores obuient, ex quo ſpacium .q.
n. à ſuo viatore conficietur, eo ipſo
tempore, quo à ſuo ſpacium .b.o. ita
que eadem erit proportio .q.n. ad .b.
proportio .d.o. ad .o.b. quæ numeri
dierum eius, qui à .b. pergit in .d. ad
numerum dierum alterius qui à .q. in
p. proficiſcitur, & componendo eadem
erit proportio .d.b. ad .b.o. quæ ſum-
mæ dierum ad minorem numerum ipſorum, & eadem quæ dierum .b.d. ad dies
ipſius .b.o.
THEOREMA CXV.
CIRCA hæc ipſa itinera aliud quæritur peruenuſtè, in quo quæſito illud con
ſtituitur cognitum eſſe, nempe interuallum inter duo diuerſa loca, è quibus
duo viatores eodem inſtanti vt ſibi occurrant proficiſcuntur, certaque; milliaria ſin-
gulis diebus conficiant, ita tamen, ut unus ordinatè plura altero ambulet, quæritur
deinde quoto die ſibi occurrent. Hoc autem fit diuiſo toto interuallo locorum per
ſummam milliariorum quam vterque quotidie abſoluit.
ſtituitur cognitum eſſe, nempe interuallum inter duo diuerſa loca, è quibus
duo viatores eodem inſtanti vt ſibi occurrant proficiſcuntur, certaque; milliaria ſin-
gulis diebus conficiant, ita tamen, ut unus ordinatè plura altero ambulet, quæritur
deinde quoto die ſibi occurrent. Hoc autem fit diuiſo toto interuallo locorum per
ſummam milliariorum quam vterque quotidie abſoluit.

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib