2816IO. BAPT. BENED.
tas vero cui differentiam .n.c. æquari dico, ſit .a.i.
Patet enim in primis, eandem propor
tionem eſſe .a.e. ad .a.c. quæ eſt .u.e. ad .a.i. ex definitione diuiſionis, et eandem
eſſe .a.u. ad .a.n. quæ eſt .u.e. ad .a.i. vnde ex .
11. quinti ſic ſe habebit .a.e. ad .a.c. ſicut .a.
 34[Figure 34]
u. ad .a.n. et ex .19. eiuſdem ſic ſe habe-
34[Figure 34]
u. ad .a.n. et ex .19. eiuſdem ſic ſe habe-
bit .u.e. ad .n.c. ſicut .a.e. ad .a.c. ſed. ſic ſe
habebat .u.e. ad .a.i. Itaque; ex prædicta .11. quinti, ſic ſe habebit .u.e. ad .n.c. ſicut ad .a.
i. Quare ex .9. eiuſdem .n.c. æqualis erit .a.i. etidcirco .n.c. pariter vnitas erit.
tionem eſſe .a.e. ad .a.c. quæ eſt .u.e. ad .a.i. ex definitione diuiſionis, et eandem
eſſe .a.u. ad .a.n. quæ eſt .u.e. ad .a.i. vnde ex .
11. quinti ſic ſe habebit .a.e. ad .a.c. ſicut .a.
bit .u.e. ad .n.c. ſicut .a.e. ad .a.c. ſed. ſic ſe
habebat .u.e. ad .a.i. Itaque; ex prædicta .11. quinti, ſic ſe habebit .u.e. ad .n.c. ſicut ad .a.
i. Quare ex .9. eiuſdem .n.c. æqualis erit .a.i. etidcirco .n.c. pariter vnitas erit.
THEOREMA XXIIII.
CVr quibuslibet duobus numeris diuiſis adinuicem, multiplicatisque prouenien
tibus ſimul, productum, ſemper eſt vnitas ſuperficialis? Nempe ex .20. ſeptimi,
quoniam vnitas linearis ſemper media proportionalis eſt inter bina prouenientia.
Quodita ſpecularilicet.
tibus ſimul, productum, ſemper eſt vnitas ſuperficialis? Nempe ex .20. ſeptimi,
quoniam vnitas linearis ſemper media proportionalis eſt inter bina prouenientia.
Quodita ſpecularilicet.
Significentur duo propoſiti numeri per .b.p. et .b.d. mutuo diuiſi, proueniens au-
tem .b.p. per .b.d. diuiſum ſit .b.n. tum proueniens .b.d. diuiſum per .b.p. ſit .b.a.
et .b.t. ſit vnitas .b.p. et .b.e. vnitas .b.d. ex quo .b.t. æqualis erit .b.e.
tem .b.p. per .b.d. diuiſum ſit .b.n. tum proueniens .b.d. diuiſum per .b.p. ſit .b.a.
et .b.t. ſit vnitas .b.p. et .b.e. vnitas .b.d. ex quo .b.t. æqualis erit .b.e.
Iam ex definitio ne diuiſionis, dabitur eadem proportio .b.p. ad .b.n. quæ eſt .b.d.
ad .b.e. et proportio .b.d. ad .b.a. quæ eſt .b.p. ad .b.t. Sed cum ſic ſe habeat .b.
p. ad .b.n. ſicut .b.d. ad .b.e. permutando ſic ſe habebit .b.p. ad .b.d. ſicut .b.n. ad .b.
e. hoc eſt ad .b.t. et cum ſic ſe habeat .b.d. ad .b.a. ſicut .b.p. ad .b.t: permutando ſic ſe
habebit .b.d. ad .b.p. ſicut .b.a. ad .b.t.
Quare euerſim ſic ſe habebit .b.p. ad .
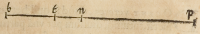 35[Figure 35]
35[Figure 35]
b.d. ſicut .b.t. ad .b.a. ſed .b.n. ad .b.t. ſic
ſe habebat vt .b.p. ad .b.d. Itaque; ex .11.
quintiſic ſe habebit .b.n. ad .b.t. ſicut .b.
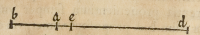 36[Figure 36]
e. ad .b.a.
Dictum autem eſt .b.e. et .b.t. idem omnino eſſe.
Quare ex .20. ſeptimi pro-
36[Figure 36]
e. ad .b.a.
Dictum autem eſt .b.e. et .b.t. idem omnino eſſe.
Quare ex .20. ſeptimi pro-
poſiti veritas innoteſcet.
ad .b.e. et proportio .b.d. ad .b.a. quæ eſt .b.p. ad .b.t. Sed cum ſic ſe habeat .b.
p. ad .b.n. ſicut .b.d. ad .b.e. permutando ſic ſe habebit .b.p. ad .b.d. ſicut .b.n. ad .b.
e. hoc eſt ad .b.t. et cum ſic ſe habeat .b.d. ad .b.a. ſicut .b.p. ad .b.t: permutando ſic ſe
habebit .b.d. ad .b.p. ſicut .b.a. ad .b.t.
Quare euerſim ſic ſe habebit .b.p. ad .
b.d. ſicut .b.t. ad .b.a. ſed .b.n. ad .b.t. ſic
ſe habebat vt .b.p. ad .b.d. Itaque; ex .11.
quintiſic ſe habebit .b.n. ad .b.t. ſicut .b.
poſiti veritas innoteſcet.
THEOREMA XXV.
IDipſum & hac altera uia patebit.
Duo illi numeri per .o. et .u. ſignificentur mutuo diuiſi, proueniens autem .o. per .
u. ſit .e. et proueniens .u. per .o. ſit .x. vnitas uerò per .i. ſignificetur, quas tamen quanti-
tates ſubſcripto modo ad inuicem diſponi-
to. Itaque; ex definitione diuiſionis, eadem erit
 37[Figure 37]
proportio .o. ad .e. quę eſt .u. ad .i. et .o. ad .i. quę
37[Figure 37]
proportio .o. ad .e. quę eſt .u. ad .i. et .o. ad .i. quę
eſt .u. ad .x. Quare ex æqualitate proportionum .
c. ad .i. ſic ſe habebit ſicut .i. ad .x. erit enim .i.
media proportionalis inter .e. et .x. ex .20. autem
ſeptimi propoſitum concludetur. Huiuſmodi rei cauſa etiam eſt, quod proueniens
diuiſionis vnius eſt numerator æqualis denominatori diuiſionis alterius.
u. ſit .e. et proueniens .u. per .o. ſit .x. vnitas uerò per .i. ſignificetur, quas tamen quanti-
tates ſubſcripto modo ad inuicem diſponi-
to. Itaque; ex definitione diuiſionis, eadem erit
eſt .u. ad .x. Quare ex æqualitate proportionum .
c. ad .i. ſic ſe habebit ſicut .i. ad .x. erit enim .i.
media proportionalis inter .e. et .x. ex .20. autem
ſeptimi propoſitum concludetur. Huiuſmodi rei cauſa etiam eſt, quod proueniens
diuiſionis vnius eſt numerator æqualis denominatori diuiſionis alterius.
THEOREMA XXVI.
CVr duobus numeris mutuo diuiſis, sumptis deinde prouenientibus ſimul et adinui
cem, & per hanc ſummam, diuiſa ſumma quadratorum dictorum propoſitorum
cem, & per hanc ſummam, diuiſa ſumma quadratorum dictorum propoſitorum

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib