388376IO. BABPT. BENED.
 429[Figure 429]
429[Figure 429]
Poſſumus etiam probare quod periferia quadrati æqualis triangulo æquilatero
minor ſit periferia ipſius trianguli æquilateri. Cogita triangulum æquilaterum hic
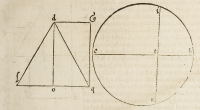
ſubſcriptum .d.l.q. cuius baſis .l.q. diuiſa ſit per æqualia à perpendiculari .d.o. deſcri-
ptumque; ſit rectangulum .o.g. quod æquale erit triangulo .d.l.q. ſed periferia trianguli
maior eſt periferia rectanguli, nam .l.q. æqualis eſt .o.q. cum .d.g. ſed .q.d. maior eſt .o.
d. ex .18. primi, vnde .l.d. maior etiam .q.g. cum ex .34. dicti latera oppoſita ipſius re
ctanguli ſint inuicem æqualia, accipiamus poſtea .e.c. æqualem .o.d. et .c.h. indire-
ctum æqualem .o.q. circa quem diametrum .e.h. intelligatur circulus .e.i.h.k. et. à pun
cto .c. dirigatur perpendicularis .k.i. ad .e.h. vnde ex .3. tertij .c.i. æqualis erit .c.k. & ex
34. quod fit ex .c.i. in .c.k. hoc eſt quadratum ipſius .c.i. æquale erit ei quod fit .ex .e.c.
in .c.h. hoc eſt rectangulo .g.o. hoc eſt triangulo .d.l.q. ſed .e.h. eſt dimidium perife-
rię ipſius rectanguli .g.o. quæ minor eſt di midio periferiæ trianguli .d.l.q. vt vidimus
et .i.k. eſt dimidium periferię quadrati ipſius .i.c. & minor etiam ipſa .e.h. ex .14. tertij
quare verum eſt propoſitum.
minor ſit periferia ipſius trianguli æquilateri. Cogita triangulum æquilaterum hic
ſubſcriptum .d.l.q. cuius baſis .l.q. diuiſa ſit per æqualia à perpendiculari .d.o. deſcri-
ptumque; ſit rectangulum .o.g. quod æquale erit triangulo .d.l.q. ſed periferia trianguli
maior eſt periferia rectanguli, nam .l.q. æqualis eſt .o.q. cum .d.g. ſed .q.d. maior eſt .o.
d. ex .18. primi, vnde .l.d. maior etiam .q.g. cum ex .34. dicti latera oppoſita ipſius re
ctanguli ſint inuicem æqualia, accipiamus poſtea .e.c. æqualem .o.d. et .c.h. indire-
ctum æqualem .o.q. circa quem diametrum .e.h. intelligatur circulus .e.i.h.k. et. à pun
cto .c. dirigatur perpendicularis .k.i. ad .e.h. vnde ex .3. tertij .c.i. æqualis erit .c.k. & ex
34. quod fit ex .c.i. in .c.k. hoc eſt quadratum ipſius .c.i. æquale erit ei quod fit .ex .e.c.
in .c.h. hoc eſt rectangulo .g.o. hoc eſt triangulo .d.l.q. ſed .e.h. eſt dimidium perife-
rię ipſius rectanguli .g.o. quæ minor eſt di midio periferiæ trianguli .d.l.q. vt vidimus
et .i.k. eſt dimidium periferię quadrati ipſius .i.c. & minor etiam ipſa .e.h. ex .14. tertij
quare verum eſt propoſitum.
Sed quando periferiæ ſunt inuicem æquales, poſſumus etiam breuiter videre id
quod ſupradiximus, hoc eſt, quod quadratum, maius ſit triangulo æquilatero. Nam
cum .b.g. ſeſquitertia ſit ad .b.a. ergo .b.g. erit vt .4. et .b.a. ut .3. vnde .b.q. erit vt .16
et .b.l. vt .9. et .c.q. vt .8. quare .b.l. maius erit ipſo rectangulo .c.q. ſed .c.q. maius eſt triam
gulo .b.o.g. cum .q.g. quæ æqualis eſt .o.g. maior ſit .o.c. ex .18. vel penultima primi,
nam ſi .q.g. æqualis eſſet .o.c. tunc .c.q. æqualis eſſet triangulo .b.o.g. ex .41. primi.
quod ſupradiximus, hoc eſt, quod quadratum, maius ſit triangulo æquilatero. Nam
cum .b.g. ſeſquitertia ſit ad .b.a. ergo .b.g. erit vt .4. et .b.a. ut .3. vnde .b.q. erit vt .16
et .b.l. vt .9. et .c.q. vt .8. quare .b.l. maius erit ipſo rectangulo .c.q. ſed .c.q. maius eſt triam
gulo .b.o.g. cum .q.g. quæ æqualis eſt .o.g. maior ſit .o.c. ex .18. vel penultima primi,
nam ſi .q.g. æqualis eſſet .o.c. tunc .c.q. æqualis eſſet triangulo .b.o.g. ex .41. primi.
Alia etiam via maiores noſtri vſi ſunt quæ generalis eſt vt in Theone ſupra Al-
mageſtum videre eſt, medijs perpendicularibus à centris ad latera figurarum, ſed
quia differentia longitudinum ipſarum perpendicularium alio medio inueniri poteſt,
eo quo ipſi vſi ſunt, prætermittere nolo quin tibi ſcribam.
mageſtum videre eſt, medijs perpendicularibus à centris ad latera figurarum, ſed
quia differentia longitudinum ipſarum perpendicularium alio medio inueniri poteſt,
eo quo ipſi vſi ſunt, prætermittere nolo quin tibi ſcribam.
Ego enim ita diſcurro.
Sint duæ figuræ iſoperimetrę æquilaterę & æquiangulæ, puta primò trian-
gulum & quadratum quorum centra ſint .e. et .o. à quibus centris ad latera ſint per-
pendiculares .e.n. et .o.u. vnde .n. et .u. diuident latera per æqualia vt ſcis, ducantur
poſtea .e.t. et .o.a. ad angulos dictorum laterum, vnde habebimus angulum .o.a.u. di-
midium recti, et .e.t.n. tertia pars vnius recti, vt ex te ipſo videre potes, quare angulus
gulum & quadratum quorum centra ſint .e. et .o. à quibus centris ad latera ſint per-
pendiculares .e.n. et .o.u. vnde .n. et .u. diuident latera per æqualia vt ſcis, ducantur
poſtea .e.t. et .o.a. ad angulos dictorum laterum, vnde habebimus angulum .o.a.u. di-
midium recti, et .e.t.n. tertia pars vnius recti, vt ex te ipſo videre potes, quare angulus

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib