392380IO. BAPT. BENED.
negotio cordarum & arcuum poſſumus geometricè demonſtrare quod valde de-
ſideras.
ſideras.
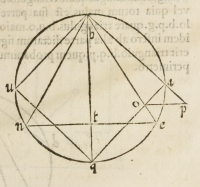
Quapropter ſit circulus .b.a.e.q. in quo ſit triangulum æquilaterum .b.e.n. & quadra
tum .b.a.q.u. cuius periferiam probabo longiorem eſſe periferia trianguli. Sit enim
diameter circuli .b.q. qui etiam erit diameter quadrati, vt à te ſcire potes. Sit etiam
punctum .b. commune tam anguli quadrati quam trianguli. vnde ſequitur quod dictus
diameter ſecabit latus .n.e. trianguli ad rectos & per æqualia in .t. Nam cum arcus .b.
e. æqualis ſit arcui .b.n. ex .27. tertij, remanet vt arcus .q.e. equalis ſit arcui .q.n. vnde
angulus .q.b.e. æqualis erit angulo .q.b.n. ex .26. eiuſdem. quare ex .4. primi anguli
ad .t. erunt recti, et .n.t. æqualis erit ipſi .t.e. vt diximus.
tum .b.a.q.u. cuius periferiam probabo longiorem eſſe periferia trianguli. Sit enim
diameter circuli .b.q. qui etiam erit diameter quadrati, vt à te ſcire potes. Sit etiam
punctum .b. commune tam anguli quadrati quam trianguli. vnde ſequitur quod dictus
diameter ſecabit latus .n.e. trianguli ad rectos & per æqualia in .t. Nam cum arcus .b.
e. æqualis ſit arcui .b.n. ex .27. tertij, remanet vt arcus .q.e. equalis ſit arcui .q.n. vnde
angulus .q.b.e. æqualis erit angulo .q.b.n. ex .26. eiuſdem. quare ex .4. primi anguli
ad .t. erunt recti, et .n.t. æqualis erit ipſi .t.e. vt diximus.
Deinde .b.e. et .q.a. ſeinuicem ſecant in puncto .o. vt ex ſe clarum patet, ducatur po
ſtea .q.e. vnde habebimus angulum .b.e.q. rectum ex .30. tertij, quare ex .18. primi .q.
o. longior erit ipſa .q.e. et .q.e. longior erit ipſa .e.t. quare .q.o. longior erit ipſa .t.e.
ſtea .q.e. vnde habebimus angulum .b.e.q. rectum ex .30. tertij, quare ex .18. primi .q.
o. longior erit ipſa .q.e. et .q.e. longior erit ipſa .e.t. quare .q.o. longior erit ipſa .t.e.
Vt probemus poſtea .b.a.o. longiorem eſſe ipſa .b.e. producatur .b.a. ita quod .a.
p. æqualis ſit ipſi .a.o. ducaturque; o.p. et .a.e. cum autem ex iam dicta .30. tertij angulus
b.a.o. rectus ſit, erit angulus .o.a.p. ſimiliter rectus ex .13. primi, vnde ex .5. et .32. eiuſdem
angulus .a.p.o. erit dimidium recti, & ſimiliter, exijſdem, angulus .b.q.a. eſt dimidium
recti quare angulus .a.p.o. æqualis erit angulo .a.q.b. ſed angulus .a.e.b. æqualis eſt an
gulo .a.q.b. ex .20. tertij, ergo angulus .b.p.o. æqualis erit angulo .b, e.a. angulus vero
a.b.e. communis eſt ambobus triangulis .a.b.e. et .o.b.p. quare ex .32. primi anguli .
b.a.e. et .b.o.p. reliqui ex duobus rectis æqua
 433[Figure 433]
les inuicem erunt.
Quare ex quarta ſexti,
433[Figure 433]
les inuicem erunt.
Quare ex quarta ſexti,
et .18. quinti proportio .b.o. ad .b.p. erit, vt
b.a. ad .b.e. ſed ex .18. primi .b.o. maior eſt
ipſa .b.a. quare ex .14. quinti .b.p. maior erit
ipſa .b.e. ſed .b.p. æquatur ipſis .b.a. cum .a. o
ex hypoteſi, ergo .b.a. cum .a.o. maior erit
ipſa .b.e. ſed .q.o. maior erat ipſa .t.e. vt ſupe
rius vidimus, quare .b.a. cum .a.o. et .o.q. ma
ior eſt ipſa .b.e. cum .e.t. hoc eſt dimidium
periferię ipſius quadrati, maius erit dimidio
periferię ipſius trianguli propoſiti, quare ex 14.
dicta tota periferia dicti trianguli, ſimiliter
probarem de omnibus alijs figuris regulari
bus eodem circulo inſcriptis.
p. æqualis ſit ipſi .a.o. ducaturque; o.p. et .a.e. cum autem ex iam dicta .30. tertij angulus
b.a.o. rectus ſit, erit angulus .o.a.p. ſimiliter rectus ex .13. primi, vnde ex .5. et .32. eiuſdem
angulus .a.p.o. erit dimidium recti, & ſimiliter, exijſdem, angulus .b.q.a. eſt dimidium
recti quare angulus .a.p.o. æqualis erit angulo .a.q.b. ſed angulus .a.e.b. æqualis eſt an
gulo .a.q.b. ex .20. tertij, ergo angulus .b.p.o. æqualis erit angulo .b, e.a. angulus vero
a.b.e. communis eſt ambobus triangulis .a.b.e. et .o.b.p. quare ex .32. primi anguli .
b.a.e. et .b.o.p. reliqui ex duobus rectis æqua
et .18. quinti proportio .b.o. ad .b.p. erit, vt
b.a. ad .b.e. ſed ex .18. primi .b.o. maior eſt
ipſa .b.a. quare ex .14. quinti .b.p. maior erit
ipſa .b.e. ſed .b.p. æquatur ipſis .b.a. cum .a. o
ex hypoteſi, ergo .b.a. cum .a.o. maior erit
ipſa .b.e. ſed .q.o. maior erat ipſa .t.e. vt ſupe
rius vidimus, quare .b.a. cum .a.o. et .o.q. ma
ior eſt ipſa .b.e. cum .e.t. hoc eſt dimidium
periferię ipſius quadrati, maius erit dimidio
periferię ipſius trianguli propoſiti, quare ex 14.
dicta tota periferia dicti trianguli, ſimiliter
probarem de omnibus alijs figuris regulari
bus eodem circulo inſcriptis.
CONSIDERATIONES NONNVLLÆ IN
Archimedem.
Archimedem.
Doct ßimo atque Reuerendo Domino Vincentio
Mercato.
Mercato.
QVod tibi aliàs dixi verum eſt, intellectum ſcilicet non omninò quieſcere cir
ca illas duas Archimedis propoſitiones, quæ in translatione Tartaleæ ſunt
ſub numeris .4. et .5. & in impreſſione Baſileæ ſub numeris .6. et .7. vbi
tractat
ca illas duas Archimedis propoſitiones, quæ in translatione Tartaleæ ſunt
ſub numeris .4. et .5. & in impreſſione Baſileæ ſub numeris .6. et .7. vbi
tractat

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib