nach diesem Index summiert (,,Verjüngung“). Man gewinnt
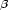
so z. B. aus dem gemischten Tensor vierten Ranges A den
gemischten Tensor zweiten

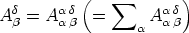
und aus diesem, abermals durch Verjüngung, den Tensor
nullten A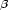 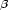= A = A.

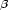
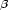Der Beweis dafür, daß das Ergebnis der Verjüngung wirk-
lich Tensorcharakter besitzt, ergibt sich entweder aus der
Tensordarstellung gemäß der Verallgemeinerung von (12) in
Verbindung mit (6) oder aus der Verallgemeinerung von (13).

Innere und gemischte Multiplikation der Tensoren. Diese
bestehen in der Kombination der äußeren Multiplikation mit
der

Beispiele. -- Aus dem kovarianten Tensor zweiten Ranges
A und dem kontravarianten Tensor ersten Ranges B bilden
wir durch äußere Multiplikation den gemischten

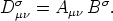
Durch Verjüngung nach den Indizes , entsteht der ko-
variante Vierervektor

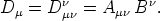
Diesen bezeichnen wir auch als inneres Produkt der Tensoren
A und B. Analog bildet man aus den Tensoren A und
B durch äußere Multiplikation und zweimalige Verjüngung
das innere Produkt A B. Durch äußere Produktbildung
und einmalige Verjüngung erhält man aus A und B den
gemischten Tensor zweiten Ranges D = A B. Man kann
diese Operation passend als eine gemischte bezeichnen; denn
sie ist eine äußere bezüglich der Indizes 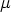und , eine innere
bezüglich der Indizes

Wir beweisen nun einen Satz, der zum Nachweis des
Tensorcharakters oft verwendbar ist. Nach dem soeben Dar-
gelegten ist A B ein Skalar, wenn A und B Tensoren
sind. Wir behaupten aber auch folgendes. Wenn A B für
jede Wahl des Tensors B eine Invariante ist, so hat A Tensor-
charakter.

Beweis. -- Es ist nach Voraussetzung für eine beliebige
Substitution

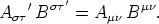
Nach der Umkehrung von (9) ist

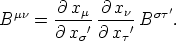
Dies, eingesetzt in obige Gleichung,

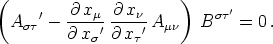
Dies kann bei beliebiger Wahl von B^' nur dann erfüllt
sein, wenn die Klammer verschwindet, woraus mit Rück-
sicht auf (11) die Behauptung

Dieser Satz gilt entsprechend für Tensoren beliebigen
Ranges und Charakters; der Beweis ist stets analog zu

Der Satz läßt sich ebenso beweisen in der Form: Sind
B und C beliebige Vektoren, und ist bei jeder Wahl der-
selben das innere Produkt

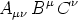
ein Skalar, so ist A ein kovarianter Tensor. Dieser letztere
Satz gilt auch dann noch, wenn nur die speziellere Aussage
zutrifft, daß bei beliebiger Wahl des Vierervektors B das
skalare

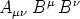
ein Skalar ist, falls man außerdem weiß, daß A der Sym-
A = A genügt. Denn auf dem vorhin
angegebenen Wege beweist man den Tensorcharakter von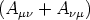
, woraus dann wegen der Symmetrieeigenschaft
der Tensorcharakter von A selbst folgt. Auch dieser Satz
läßt sich leicht verallgemeinern auf den Fall kovarianter und
kontravarianter Tensoren beliebigen

Endlich folgt aus dem Bewiesenen der ebenfalls auf be-
liebige Tensoren zu verallgemeinernde Satz: Wenn die Größen
A B bei beliebiger Wahl des Vierervektors B einen Tensor
ersten Ranges bilden, so ist A ein Tensor zweiten Ranges.
Ist nämlich C ein beliebiger Vierervektor, so ist wegen des
Tensorcharakters A B das innere Produkt A C B bei
beliebiger Wahl der beiden Vierervektoren C und B ein
Skalar, woraus die Behauptung

Der kovariante Fundamentaltensor. In dem invarianten
Ausdruck des Quadrates des Linienelementes

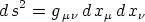
spielt d x die Rolle eines beliebig wählbaren kontravarianten
Vektors. Da g = g, so folgt nach den Betrachtungen
des letzten Paragraphen hieraus, daß g ein kovarianter Tensor
zweiten Ranges ist. Wir nennen ihn ,,Fundamentaltensor“.
Im folgenden leiten wir einige Eigenschaften dieses Tensors
ab, die zwar jedem Tensor zweiten Ranges eigen sind; aber
die besondere Rolle des Fundamentaltensors in unserer Theorie,
welche in der Besonderheit der Gravitationswirkungen ihren
physikalischen Grund hat, bringt es mit sich, daß die zu ent-
wickelnden Relationen nur bei dem Fundamentaltensor für
uns von Bedeutung

Der kontravariante Fundamentaltensor. Bildet man in dem
Determinantenschema der g zu jedem g die Unterdetermi-
nante und dividiert diese durch die Determinante g = 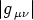der
g, so erhält man gewisse Größen g(= g ), von denen wir
beweisen wollen, daß sie einen kontravarianten Tensor

Nach einem bekannten Determinantensatze ist

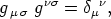(16)

wobei das Zeichen 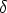1 oder 0 bedeutet, je nachdem =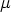
oder 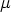ist. Statt des obigen Ausdruckes für d s² können
wir

oder nach (16) auch

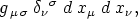
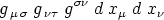
schreiben. Nun bilden aber nach den Multiplikationsregeln
des vorigen Paragraphen die

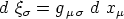
einen kovarianten Vierervektor, und zwar (wegen der will-
kürlichen Wählbarkeit der d x) einen beliebig wählbaren
Vierervektor. Indem wir ihn in unseren Ausdruck einführen,
erhalten wir

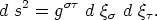
Da dies bei beliebiger Wahl des Vektors d ein Skalar
ist und g nach seiner Definition in den Indizes und sym-
metrisch ist, folgt aus den Ergebnissen des vorigen Para-
graphen, daß g ein kontravarianter Tensor ist. Aus (16)
folgt noch, daß auch 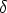ein Tensor ist, den wir den gemischten
Fundamentaltensor nennen können.