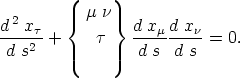(22)

Hierbei ist nach Christoffel gesetzt

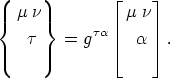(23)

Gestützt auf die Gleichung der geodätischen Linie können
wir nun leicht die Gesetze ableiten, nach welchen durch Diffe-
rentiation aus Tensoren neue Tensoren gebildet werden können.
Dadurch werden wir erst in den Stand gesetzt, allgemein ko-
variante Differentialgleichungen aufzustellen. Wir erreichen
dies Ziel durch wiederholte Anwendung des folgenden ein-
fachen Satzes.

Ist in unserem Kontinuum eine Kurve gegeben, deren
Punkte durch die Bogendistanz s von einem Fixpunkt auf
der Kurve charakterisiert sind, ist ferner 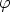eine invariante
Raumfunktion, so ist auch d 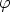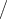d s eine Invariante. Der Be-
weis liegt darin, daß sowohl d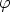 als auch ds Invariante

Da

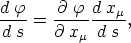
so ist auch

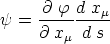
eine Invariante, und zwar für alle Kurven, die von einem
Punkte des Kontinuums ausgehen, d. h. für beliebige Wahl
des Vektors der d x. Daraus folgt unmittelbar, daß

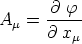(24)

ein kovarianter Vierervektor ist (Gradient von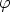

Nach unserem Satze ist ebenso der auf einer Kurve ge-
nommene Differentialquotient

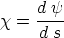
eine Invariante. Durch Einsetzen von 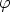erhalten wir

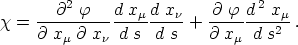
Hieraus läßt sich zunächst die Existenz eines Tensors
nicht ableiten. Setzen wir nun aber fest, daß die Kurve,