List of thumbnails
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
auf welcher wir differenziiert haben, eine geodätische Kurve
sei, so erhalten wir nach (22) durch Ersetzen von d2 x
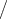 d s2
d s2
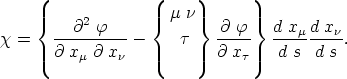
Aus der Vertauschbarkeit der Differentiationen nach 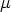
und  und daraus, daß gemäß (23) und (21) die Klammer
und daraus, daß gemäß (23) und (21) die Klammer 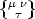
bezüglich 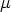 und
und  symmetrisch ist, folgt, daß der Klammer-
symmetrisch ist, folgt, daß der Klammer-
ausdruck in 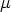 und
und  symmetrisch ist. Da man von einem
symmetrisch ist. Da man von einem
Punkt des Kontinuums aus in beliebiger Richtung eine geo-
dätische Linie ziehen kann, d x
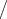 d s also ein Vierervektor mit
d s also ein Vierervektor mit
frei wählbarem Verhältnis der Komponenten ist, folgt nach
den Ergebnissen des § 7, daß
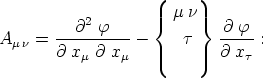 | (25) |
ein kovarianter Tensor zweiten Ranges ist. Wir haben also
das Ergebnis gewonnen: Aus dem kovarianten Tensor ersten
Ranges
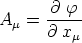
können wir durch Differentiation einen kovarianten Tensor
zweiten Ranges
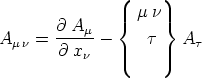 | (26) |
bilden. Wir nennen den Tensor A
 die ,,Erweiterung“ des
die ,,Erweiterung“ des
Tensors A . Zunächst können wir leicht zeigen, daß diese
. Zunächst können wir leicht zeigen, daß diese
Bildung auch dann auf einen Tensor führt, wenn der Vektor A
nicht als ein Gradient darstellbar ist. Um dies einzusehen,
bemerken wir zunächst, daß
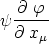
ein kovarianter Vierervektor ist, wenn 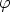 und
und 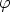 Skalare sind.
Skalare sind.
Dies ist auch der Fall für eine aus vier solchen Gliedern be-
stehende
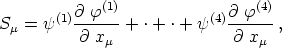
falls 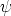 (1)
(1) 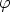 (1)....
(1)....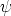 (4)
(4) 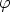 (4) Skalare sind. Nun ist aber klar, daß
(4) Skalare sind. Nun ist aber klar, daß
sich jeder kovariante Vierervektor in der Form S darstellen
darstellen
läßt. Ist nämlich A ein Vierervektor, dessen Komponenten
ein Vierervektor, dessen Komponenten