beliebig gegebene Funktionen der x sind, so hat man nur
(bezüglich des gewählten Koordinatensystems) zu

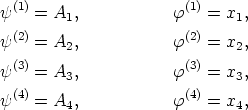
um zu erreichen, daß S gleich A

Um daher zu beweisen, daß A ein Tensor ist, wenn auf
der rechten Seite A ein beliebiger kovarianter Vierer-
vektor eingesetzt wird, brauchen wir nur zu zeigen, daß dies
für den Vierervektor S zutrifft. Für letzteres ist es aber,
wie ein Blick auf die rechte Seite von (26) lehrt, hinreichend,
den Nachweis für den Fall

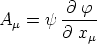
zu führen. Es hat nun die mit 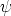multiplizierte rechte Seite
von (25)

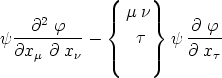
Tensorcharakter. Ebenso ist

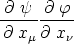
ein Tensor (äußeres Produkt zweier Vierervektoren). Durch
Addition folgt der Tensorcharakter

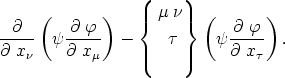
Damit ist, wie ein Blick auf (26) lehrt, der verlangte Nachweis
für den

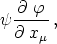
und daher nach dem vorhin Bewiesenen für jeden beliebigen
Vierervektor A geführt.

Mit Hilfe der Erweiterung des Vierervektors kann man
leicht die ,,Erweiterung“ eines kovarianten Tensors beliebigen
Ranges definieren; diese Bildung ist eine Verallgemeinerung
der Erweiterung des Vierervektors. Wir beschränken uns auf
die Aufstellung der Erweiterung des Tensors zweiten Ranges,
da dieser das Bildungsgesetz bereits klar übersehen