Wie bereits bemerkt, läßt sich jeder kovariante Tensor
zweiten Ranges darstellen¹) als eine Summe von Tensoren
vom Typus A B. Es wird deshalb genügen, den Ausdruck
der Erweiterung für einen solchen speziellen Tensor abzuleiten.
Nach (26) haben die

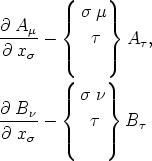
Tensorcharakter. Durch äußere Multiplikation des ersten mit
B, des zweiten A erhält man je einen Tensor dritten
Ranges; deren Addition ergibt den Tensor dritten Ranges

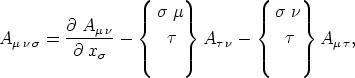(27)

wobei A = A B gesetzt ist. Da die rechte Seite von (27)
linear und homogen ist bezüglich der A und deren ersten
Ableitungen, führt dieses Bildungsgesetz nicht nur bei einem
Tensor vom Typus A B, sondern auch bei einer Summe
solcher Tensoren, d. h. bei einem beliebigen kovarianten
Tensor zweiten Ranges, zu einem Tensor. Wir nennen A
die Erweiterung des A.

Es ist klar, daß (26) und (24) nur spezielle Fälle von (27)
sind (Erweiterung des Tensors ersten bzw. nullten Ranges).
Überhaupt lassen sich alle speziellen Bildungsgesetze von
Tensoren auf (27) in Verbindung mit Tensormultiplikationen

Einige den Fundamentaltensor betreffende Hilfssätze. Wir
leiten zunächst einige im folgenden viel gebrauchte Hilfs-

1) Durch äußere Multiplikation der Vektoren mit den (beliebig
gegebenen) Komponenten A₁₁, A₁₂, A₁₃, A₁₄ bzw. 1, 0, 0, 0 entsteht
ein Tensor mit den

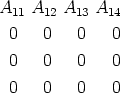
Durch Addition von vier Tensoren von diesem Typus erhält man den
Tensor A mit beliebig vorgeschriebenen Komponenten.