Der klassischen Mechanik und nicht minder der speziellen
Relativitätstheorie haftet ein erkenntnistheoretischer Mangel
an, der vielleicht zum ersten Male von E. Mach klar hervor-
gehoben wurde. Wir erläutern ihn am folgenden Beispiel.
Zwei flüssige Körper von gleicher Größe und Art schweben
frei im Raume in so großer Entfernung voneinander (und von
allen übrigen Massen), daß nur diejenigen Gravitationskräfte
berücksichtigt werden müssen, welche die Teile eines dieser
Körper aufeinander ausüben. Die Entfernung der Körper
voneinander sei unveränderlich. Relative Bewegungen der
Teile eines der Körper gegeneinander sollen nicht auftreten.
Aber jede Masse soll -- von einem relativ zu der anderen Masse
ruhenden Beobachter aus beurteilt -- um die Verbindungslinie
der Massen mit konstanter Winkelgeschwindigkeit rotieren (es
ist dies eine konstatierbare Relativbewegung beider Massen).
Nun denken wir uns die Oberflächen beider Körper (S₁ und S₂)
mit Hilfe (relativ ruhender) Maßstäbe ausgemessen; es ergebe
sich, daß die Oberfläche von S₁ eine Kugel, die von S₂ ein
Rotationsellipsoid

Wir fragen nun: Aus welchem Grunde verhalten sich die
Körper S₁ und S₂ verschieden? Eine Antwort auf diese Frage
kann nur dann als erkenntnistheoretisch befriedigend¹) an-
erkannt werden, wenn die als Grund angegebene Sache eine
beobachtbare Erfahrungstatsache ist; denn das Kausalitäts-
gesetz hat nur dann den Sinn einer Aussage über die Er-
fahrungswelt, wenn als Ursachen und Wirkungen letzten
Endes nur beobachtbare Tatsachen

Die Newtonsche Mechanik gibt auf diese Frage keine
befriedigende Antwort. Sie sagt nämlich folgendes. Die Ge-
setze der Mechanik gelten wohl für einen Raum R₁, gegen
welchen der Körper S₁ in Ruhe ist, nicht aber gegenüber einem
Raume R₂, gegen welchen S₂ in Ruhe ist. Der berechtigte
Galileische Raum R₁, der hierbei eingeführt wird, ist aber
eine blo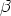 fingierte Ursache, keine beobachtbare Sache. Es
ist also klar, daß die Newtonsche Mechanik der Forderung

1) Eine derartige erkenntnistheoretisch befriedigende Antwort kann
natürlich immer noch physikalisch unzutreffend sein, falls sie mit anderen
Erfahrungen im Widerspruch ist.