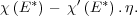- Text
- Text Image
- Image
- XML
- Thumbnail overview
- Document information
Zwei in Wechselwirkung stehende Systeme, welche diese Be-
dingung erfüllen, nennen wir zwei sich berührende Systeme.
Wir setzen noch voraus, daß 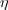 gegen H unendlich klein
gegen H unendlich klein
Für die Anzahl dN1 der N-Systeme, deren Zustands-
variabeln II1 ... II
 1 ...
1 ...  l in den Grenzen zwischen
l in den Grenzen zwischen
II1 und II1 + dII1, II2 und II2 + dII2 ... II II
II + dII
+ dII
und  1 und
1 und  1 + d
1 + d 1,
1,  2 und
2 und  2 + d
2 + d 2 ...
2 ...  l und
l und  1 + d
1 + d l
l
liegen, ergibt sich der
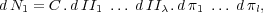
wobei C eine Funktion von E = H + 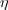 sein
sein
Da aber nach der obigen Annahme die Energie eines
jeden betrachteten Systems bis auf unendlich kleines den
Wert E* besitzt, so können wir, ohne an dem Resultat etwas
zu ändern, C durch konst. e-2 h E*
= konst.e-2 h (H+ ) ersetzen,
) ersetzen,
wobei h eine noch näher zu definierende Konstante bedeutet.
Der Ausdruck für dN1 geht also über
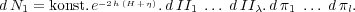
Die Anzahl der Systeme, deren Zustandsvariabeln  zwischen
zwischen
den angedeuteten Grenzen liegen, während die Werte der
Variabeln II keiner beschränkenden Bedingung unterworfen
sind, wird sich also in der
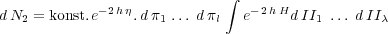
darstellen lassen, wobei das Integral über alle Werte der II
auszudehnen ist, denen Werte der Energie H zukommen, welche
zwischen E*- 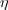 E* +
E* + 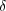 E*-
E*- 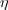 gelegen sind. Wäre die
gelegen sind. Wäre die
Integration ausgeführt, so hätten wir die Zustandsverteilung
der Systeme  gefunden. Dies ist nun tatsächlich
gefunden. Dies ist nun tatsächlich
Wir
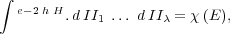
wobei die Integration auf der linken Seite über alle Werte
der Variabeln zu erstrecken ist, für welche H zwischen den be-
stimmten Werten E und E + 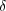 E*
liegt. Das Integral, welches
E*
liegt. Das Integral, welches
im Ausdruck dN2 auftritt, nimmt dann die Form
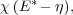
oder, da 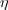 gegen E* unendlich klein
gegen E* unendlich klein