List of thumbnails
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
gemacht wird, daß in der Nähe der Zeiten t = t0 und t = t1
die auf den Körper wirkenden Kräfte von der Zeit unabhängig
seien, derart, daß für alle Punkte des starren Körpers zwischen
den
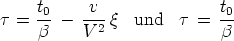
bez.
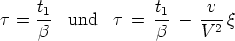
die elektrische Kraft X' von der Zeit unabhängig ist. Nennt
man X0'
bez. X1' die in diesen beiden Zeiträumen vor-
handenen X', so erhält
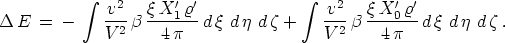
Nimmt man ferner an, daß am Anfang (t = t0) keine Kräfte
auf den Körper wirken, so verschwindet das zweite dieser
Integrale. Mit Rücksicht darauf,
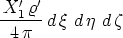
die 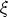 -Komponente K
-Komponente K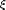 der auf das Raumelement wirkenden
der auf das Raumelement wirkenden
ponderomotorischen Kraft ist, erhält
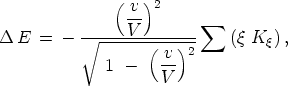
wobei die Summe über alle Massenelemente des Körpers zu
erstrecken
Wir haben also folgendes merkwürdige Resultat erhalten.
Setzt man einen starren Körper, auf den ursprünglich keine
Kräfte wirken, dem Einflusse von Kräften aus, welche dem
Körper keine Beschleunigung erteilen, so leisten diese Kräfte
-- von einem relativ zu dem Körper bewegten Koordinaten-
system aus betrachtet -- eine Arbeit 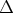 E auf den Körper,
E auf den Körper,
welche lediglich abhängt von der endgültigen Kräfteverteilung
und der Translationsgeschwindigkeit. Nach dem Energieprinzip
folgt hieraus unmittelbar, daß die kinetische Energie eines
Kräften unterworfenen starren Körpers um 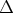 E größer ist als
E größer ist als