tritt. Betände diese letztere Wechselwirkung allein, so wäre
der quadratische Mittelwert der Bewegungsgröße der fort-
schreitenden Bewegung des Oszillators durch die statistische
Mechanik vollkommen bestimmt. In unserem Falle besteht
außerdem die Wechselwirkung des Oszillators mit dem Strah-
lungsfelde. Damit statistisches Gleichgewicht möglich sei,
darf diese letztere Wechselwirkung an jenem Mittelwerte nichts
ändern. Mit anderen Worten: der quadratische Mittelwert
der Bewegungsgröße der fortschreitenden Bewegung, welchen
der Oszillator unter der Einwirkung der Strahlung allein an-
nimmt, muß derselbe sein wie derjenige, welchen er nach der
statistischen Mechanik unter der mechanischen Einwirkung der
Moleküle allein annähme. Damit reduziert sich das Problem
auf dasjenige, den quadratischen Mittelwert (mv)2 der Be-
wegungsgröße zu ermitteln, den der Oszillator unter der Ein-
wirkung des Strahlungsfeldes allein
Dieser Mittelwert muß zur Zeit t = 0 derselbe sein wie
zur Zeit t =  , so daß man
, so daß man
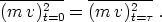
Für das folgende ist es zweckmäßig, zweierlei Kraft-
wirkungen zu unterscheiden, durch welche das Strahlungsfeld
den Oszillator beeinflußt,
1. Die Widerstandskraft K, welche der Strahlungsdruck
einer geradlinigen Bewegung des Oszillators entgegenstellt.
Diese ist bei Vernachlässigung der Glieder von Größenordnung
(v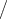 c)2 (c = Lichtgeschwindigkeit) proportional der Geschwindig-
c)2 (c = Lichtgeschwindigkeit) proportional der Geschwindig-
keit v, wir können also schreiben: K = -P v. Nehmen wir
ferner an, daß während der Zeit  die Geschwindigkeit v sich
die Geschwindigkeit v sich
nicht merklich ändert, so wird der von dieser Kraft her-
rührende Impuls = -P v 
2. Die Schwankungen 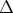 des elektromagnetischen Im-
des elektromagnetischen Im-
pulses, die infolge der Bewegung elektrischer Massen im un-
geordneten Strahlungsfelde auftreten. Diese können ebensowohl
positiv, wie negativ sein und sind von dem Umstande, daß
der Oszillator bewegt ist, in erster Annäherung
Diese Impulse superponieren sich während der Zeit  auf
auf
den Impuls (m )t=0
und unsere Gleichung wird:
)t=0
und unsere Gleichung wird:
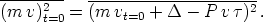 | (1) |