Es erübrigt noch die Mittelwerte der Amplituden B 0 T 2 und
0 T 2 und
C 0 T 2 durch die Strahlungsdichte
0 T 2 durch die Strahlungsdichte 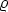
 0
0
Zu diesem Zweck müssen wir wieder die von den ver-
schiedenen Richtungen herkommende Strahlung betrachten und,
wie oben, die Amplitude der aus einer bestimmten Richtung
kommenden Strahlung mit der Energiedichte in Beziehung
setzen durch die
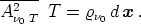
Die Amplitude:
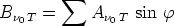
über alle Einfallswinkel, also
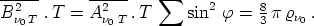 | (13) |
Analog ergibt
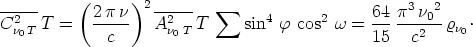 | (14) |
So erhalten wir schließlich durch Einsetzen von (13) und (14)
in (12):
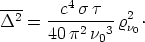 | (15) |
§ 5. Das Strahlungsgesetz.
Wir haben jetzt nur noch die gefundenen Werte (9)
und (15) in unsere Gleichung (2) einzusetzen, so gelangen wir
zu der das Strahlungsgesetz enthaltenden
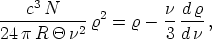
welche integriert
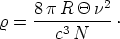 | (16) |
Dies ist das wohlbekannte Rayleighsche Strahlungsgesetz,
welches mit der Erfabrung im grellsten Widerspruche steht.
In den Grundlagen unserer Ableitung muß also eine Aussage
stecken, welche sich mit den wirklichen Erscheinungen bei
der Temperaturstrahlung nicht im Einklang
Betrachten wir darum diese Grundlagen kritisch
Man hat den Grund dafür, daß alle exakten statistischen
Betrachtungen im Gebiete der Strahlungslehre zum Rayleigh-