List of thumbnails
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
damit es trotz der Wirkung der Schwere dauernd suspendiert
bleibe. Wir können uns dabei auf den Fall beschränken, daß
das Teilchen spezifisch schwerer ist als die Flüssigkeit, da der
entgegengesetzte Fall vollkommen analog
Ist v das Volumen des Teilchens, 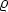 dessen Dichte,
dessen Dichte, 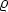 0 die
0 die
Dichte der g die Beschleunigung der Schwere und
x der vertikale Abstand eines Punktes vom Boden des Ge-
fäßes, so ergibt Gleichung
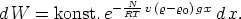
Man wird also dann finden, daß suspendierte Teilchen in
einer Flüssigkeit zu schweben vermögen, wenn für Werte
von x, die nicht wegen ihrer Kleinheit sich der Beobachtung
entziehen, die
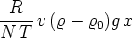
keinen allzu großen Wert besitzt -- vorausgesetzt, daß an den
Gefäßboden gelangende Teilchen nicht durch irgendwelche Um-
stände an demselben festgehalten
§ 3. Über die von der Wärmebewegung verursachten
Veränderungen des Parameters 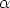 .
.
Wir kehren wieder zu dem in § 1 behandelten allgemeinen
Falle zurück, für den wir Gleichung (I) abgeleitet haben. Der
einfacheren Ausdrucksweise und Vorstellung halber wollen wir
aber nun annehmen, daß eine sehr große Zahl (n) identischer
Systeme von der dort charakterisierten Art vorliege; wir haben
es dann mit Anzahlen statt mit Wahrscheinlichkeiten zu tun.
Gleichung (I) sagt dann
Von N Systemen liegt bei
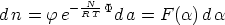 | (Ia) |
Systemen der Wert des Parameters 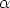 in einem zufällig heraus-
in einem zufällig heraus-
gegriffenen Zeitpunkt zwischen 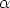 und
und 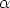 + d
+ d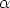 .
.
Diese Beziehung wollen wir dazu benutzen, die Größe der
durch die ungeordneten Wärmevorgänge erzeugten unregel-
mäßigen Veränderungen des Parameters 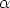 zu ermitteln. Zu
zu ermitteln. Zu
diesem Zweck drücken wir in Zeichen aus, daß die Funktion F 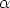 )
)