List of thumbnails
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Widerspruch steht, während Kurve I, die auf der Annahme
einer Nullpunktsenergie basiert, die Resultate der Messungen
in vorzüglicher Weise widergibt. Um festzustellen, welchen
Wert nach Formel (4)  für die Grenze T = 0 annimmt,
für die Grenze T = 0 annimmt,
schreiben wir (4) in folgender
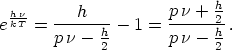
Dann sieht man, daß für T = 0  nicht gleich Null werden
nicht gleich Null werden
kann, da die rechte Seite dann gegen -1 konvergieren würde,
während auf der linken eine Potenz e steht. Es muß also
für lim T = 0  endlich bleiben, und zwar muß die rechte
endlich bleiben, und zwar muß die rechte
Seite ebenso wie die linke gegen 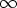 konvergieren, es muß
konvergieren, es muß
daher p 0 - h
0 - h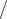 2 = 0 sein, falls wir mit
2 = 0 sein, falls wir mit  0 den Grenzwert
0 den Grenzwert
von  für T = 0 bezeichnen. Es ist
für T = 0 bezeichnen. Es ist  0 = h
0 = h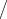 2 p. Im vor-
2 p. Im vor-
liegenden Falle ergibt sich  0 zu 11, 3.1012. Der Wert von
0 zu 11, 3.1012. Der Wert von 
ändert sich zunächst auch sehr wenig mit steigender Tempe-
ratur; so ist bei 1020
abs.  = 11, 4.1012, bei 1890
= 11, 4.1012, bei 1890  = 12, 3.1012 ,
= 12, 3.1012 ,
bei 3230  = 14, 3.1012. Dies erklärt nun, weshalb Eucken
= 14, 3.1012. Dies erklärt nun, weshalb Eucken
seine Messungen verhältnismäßig noch am besten durch die
einfache Einsteinsche Formel mit von der Temperatur un-
abhängigem  (Kurve III, Fig. 2) darstellen konnte. Jedoch
(Kurve III, Fig. 2) darstellen konnte. Jedoch
sieht man, daß auch diese Formel, namentlich bei höheren
Temperaturen, versagt, abgesehen davon, daß ohne die An-
nahme der Nullpunktsenergie die Konstanz von  völlig un-
völlig un-
verständlich bleibt. Man sieht also, daß die spezifische Wärme
des Wasserstoffs die Existenz einer Nullpunktsenergie wahr-
scheinlich macht, und es handelt sich nur noch darum, zu
prüfen, wie weit der spezielle Wert von h
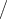 2 als gesichert
2 als gesichert
anzusehen ist. Da nun in der folgenden Untersuchung über
das Strahlungsgesetz der Betrag der Nullpunktsenergie zu h
angenommen werden muß, haben wir die spezifische Wärme des
Wasserstoffs auch für diese Annahme berechnet (p = 5, 60.10-40,
Kurve IV, Fig. 2). Es ist ersichtlich, daß die Kurve bei
höheren Temperaturen zu steil und zu hoch ist. Andererseits
ist zu bemerken, daß bei Berücksichtigung der Geschwindig-
keitsverteilung unter den Molekülen die Kurve jedenfalls etwas
flacher ausfallen dürfte. Es ist demnach zwar unwahrschein-