List of thumbnails
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
nach diesem Index summiert (,,Verjüngung“). Man gewinnt
so z. B. aus dem gemischten Tensor vierten Ranges A
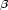

 den
den
gemischten Tensor zweiten
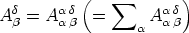
und aus diesem, abermals durch Verjüngung, den Tensor
nullten A = A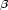
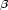 = A
= A
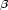

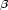 .
.
Der Beweis dafür, daß das Ergebnis der Verjüngung wirk-
lich Tensorcharakter besitzt, ergibt sich entweder aus der
Tensordarstellung gemäß der Verallgemeinerung von (12) in
Verbindung mit (6) oder aus der Verallgemeinerung von (13).
Innere und gemischte Multiplikation der Tensoren. Diese
bestehen in der Kombination der äußeren Multiplikation mit
der
Beispiele. -- Aus dem kovarianten Tensor zweiten Ranges
A
 und dem kontravarianten Tensor ersten Ranges B
und dem kontravarianten Tensor ersten Ranges B bilden
bilden
wir durch äußere Multiplikation den gemischten
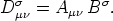
Durch Verjüngung nach den Indizes  ,
,  entsteht der ko-
entsteht der ko-
variante Vierervektor
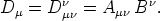
Diesen bezeichnen wir auch als inneres Produkt der Tensoren
A
 und B
und B . Analog bildet man aus den Tensoren A
. Analog bildet man aus den Tensoren A
 und
und
B
 durch äußere Multiplikation und zweimalige Verjüngung
durch äußere Multiplikation und zweimalige Verjüngung
das innere Produkt A
 B
B
 . Durch äußere Produktbildung
. Durch äußere Produktbildung
und einmalige Verjüngung erhält man aus A
 und B
und B
 den
den
gemischten Tensor zweiten Ranges D
 = A
= A
 B
B
 . Man kann
. Man kann
diese Operation passend als eine gemischte bezeichnen; denn
sie ist eine äußere bezüglich der Indizes 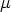 und
und  , eine innere
, eine innere
bezüglich der Indizes 

Wir beweisen nun einen Satz, der zum Nachweis des
Tensorcharakters oft verwendbar ist. Nach dem soeben Dar-
gelegten ist A
 B
B
 ein Skalar, wenn A
ein Skalar, wenn A
 und B
und B
 Tensoren
Tensoren
sind. Wir behaupten aber auch folgendes. Wenn A
 B
B
 für
für
jede Wahl des Tensors B
 eine Invariante ist, so hat A
eine Invariante ist, so hat A
 Tensor-
Tensor-
charakter.
Beweis. -- Es ist nach Voraussetzung für eine beliebige
Substitution
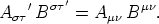
Nach der Umkehrung von (9) ist
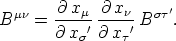
Dies, eingesetzt in obige Gleichung,
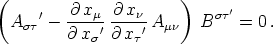
Dies kann bei beliebiger Wahl von B
 ' nur dann erfüllt
' nur dann erfüllt
sein, wenn die Klammer verschwindet, woraus mit Rück-
sicht auf (11) die Behauptung
Dieser Satz gilt entsprechend für Tensoren beliebigen
Ranges und Charakters; der Beweis ist stets analog zu
Der Satz läßt sich ebenso beweisen in der Form: Sind
B und C
und C beliebige Vektoren, und ist bei jeder Wahl der-
beliebige Vektoren, und ist bei jeder Wahl der-
selben das innere Produkt
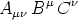
ein Skalar, so ist A
 ein kovarianter Tensor. Dieser letztere
ein kovarianter Tensor. Dieser letztere
Satz gilt auch dann noch, wenn nur die speziellere Aussage
zutrifft, daß bei beliebiger Wahl des Vierervektors B das
das
skalare
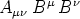
ein Skalar ist, falls man außerdem weiß, daß A
 der Sym-
der Sym-
A
 = A
= A
 genügt. Denn auf dem vorhin
genügt. Denn auf dem vorhin
angegebenen Wege beweist man den Tensorcharakter von 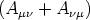 , woraus dann wegen der Symmetrieeigenschaft
, woraus dann wegen der Symmetrieeigenschaft
der Tensorcharakter von A
 selbst folgt. Auch dieser Satz
selbst folgt. Auch dieser Satz
läßt sich leicht verallgemeinern auf den Fall kovarianter und
kontravarianter Tensoren beliebigen
Endlich folgt aus dem Bewiesenen der ebenfalls auf be-
liebige Tensoren zu
verallgemeinernde Satz: Wenn die Größen
A
 B
B bei beliebiger Wahl des Vierervektors B
bei beliebiger Wahl des Vierervektors B einen Tensor
einen Tensor
ersten Ranges bilden, so ist A
 ein Tensor zweiten Ranges.
ein Tensor zweiten Ranges.
Ist nämlich C ein beliebiger Vierervektor, so ist wegen des
ein beliebiger Vierervektor, so ist wegen des
Tensorcharakters A
 B
B das innere Produkt A
das innere Produkt A
 C
C B
B bei
bei
beliebiger Wahl der beiden Vierervektoren C und B
und B ein
ein
Skalar, woraus die Behauptung
§ 8. Einiges über den Fundamentaltensor der g
 .
.
Der kovariante Fundamentaltensor. In dem invarianten
Ausdruck des Quadrates des Linienelementes
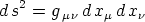
spielt d x die Rolle eines beliebig wählbaren kontravarianten
die Rolle eines beliebig wählbaren kontravarianten
Vektors. Da g
 = g
= g
 , so folgt nach den Betrachtungen
, so folgt nach den Betrachtungen
des letzten Paragraphen hieraus, daß g
 ein kovarianter Tensor
ein kovarianter Tensor
zweiten Ranges ist. Wir nennen ihn ,,Fundamentaltensor“.
Im folgenden leiten wir einige Eigenschaften dieses Tensors
ab, die zwar jedem Tensor zweiten Ranges eigen sind; aber
die besondere Rolle des Fundamentaltensors in unserer Theorie,
welche in der Besonderheit der Gravitationswirkungen ihren
physikalischen Grund hat, bringt es mit sich, daß die zu ent-
wickelnden Relationen nur bei dem Fundamentaltensor für
uns von Bedeutung
Der kontravariante Fundamentaltensor. Bildet man in dem
Determinantenschema der g
 zu jedem g
zu jedem g
 die Unterdetermi-
die Unterdetermi-
nante und dividiert diese durch die Determinante g = 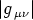 der
der
g
 , so erhält man gewisse Größen g
, so erhält man gewisse Größen g
 (= g
(= g
 ), von denen wir
), von denen wir
beweisen wollen, daß sie einen kontravarianten Tensor
Nach einem bekannten Determinantensatze ist
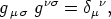 | (16) |
wobei das Zeichen 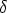

 1 oder 0 bedeutet, je nachdem
1 oder 0 bedeutet, je nachdem 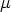 =
= 
oder 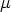
 ist. Statt des obigen Ausdruckes für d s2 können
ist. Statt des obigen Ausdruckes für d s2 können
wir
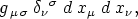
oder nach (16) auch
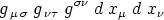
schreiben. Nun bilden aber nach den Multiplikationsregeln
des vorigen Paragraphen die
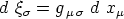
einen kovarianten Vierervektor, und zwar (wegen der will-
kürlichen Wählbarkeit der d x ) einen beliebig wählbaren
) einen beliebig wählbaren
Vierervektor. Indem wir ihn in unseren Ausdruck einführen,
erhalten wir
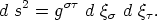
Da dies bei beliebiger Wahl des Vektors d 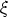
 ein Skalar
ein Skalar
ist und g
 nach seiner Definition in den Indizes
nach seiner Definition in den Indizes  und
und  sym-
sym-
metrisch ist, folgt aus den Ergebnissen des vorigen Para-
graphen, daß g
 ein kontravarianter Tensor ist. Aus (16)
ein kontravarianter Tensor ist. Aus (16)
folgt noch, daß auch 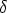

 ein Tensor ist, den wir den gemischten
ein Tensor ist, den wir den gemischten
Fundamentaltensor nennen können.