List of thumbnails
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
zwischen 0 und 0 + 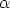 ,
,  und
und  +
+ 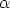 , 2
, 2  und 2
und 2  +
+ 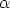 etc. (wo-
etc. (wo-
bei 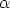 unendlich klein sei gegen
unendlich klein sei gegen  ) sei
) sei 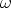 von Null verschieden,
von Null verschieden,
derart,
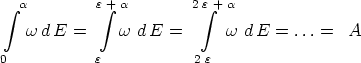
sei. Diese Festsetzung involviert, wie man aus Gleichung (3)
sieht, die Annahme, daß die Energie des betrachteten Ele-
mentargebildes lediglich solche Werte annehme, die den
Werten 0,  , 2
, 2  etc. unendlich nahe
etc. unendlich nahe
Unter Benutzung der eben dargelegten Festsetzung für 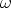
erhält man mit Hilfe von (3):
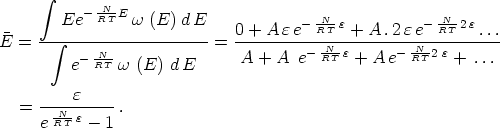
Setzt man noch  = (R/N)
= (R/N) 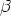
 (gemäß der Quantenhypothese),
(gemäß der Quantenhypothese),
so erhalt man hieraus:
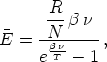 | (7) |
sowie mit Hilfe von (5) die Plancksche
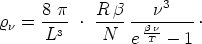
Gleichung (7) gibt die Abhängigkeit der mittleren Energie des
Planckschen Resonators von der Temperatur an.
----------
Aus dem Vorhergehenden geht klar hervor, in welchem
Sinne die molekular-kinetische Theorie der Wärme modifiziert
werden muß, um mit dem Verteilungsgesetz der schwarzen
Strahlung in Einklang gebracht zu werden. Während man
sich nämlich bisher die molekularen Bewegungen genau den-
selben Gesetzmäßigkeiten unterworfen dachte, welche fur die
Bewegungen der Körper unsever Sinnenwelt gelten (wir fügen