List of thumbnails
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
mit p den Vektor des Dipolmomentes, so erhält man fült die
X-Komponente der gesuchten Kraft den
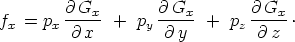
Denkt man sich den letzten Ausdruck für alle Dipole in der
Volumeneinheit gebildet und summiert, so erhält man unter
Berücksichtigung der
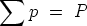
die Gleichung:
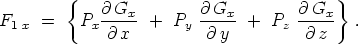 | (4) |
Wenn die algebraische Summe der positiven und negativen
Leitungselektronen nicht verschwindet, dann kommt zum Aus-
druck (4) noch ein Term hinzu, den wir nun berechnen wollen.
Die X-Komponente der auf ein Leitungselektron von der elek-
trischen Masse e wirkenden ponderomotorischen Kraft ist eGx.
Summiert man über alle Leitungselektronen der Volumen-
einheit, so erhält man:
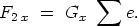 | (5) |
Denkt man sich die betrachtete in der Volumeneinheit befind-
liche Materie von einer Fläche umschlossen, welche keine
Dipole schneidet, so erhält man nach dem Gaussschen Satz
und nach der Definition des Verschiebungsvektors
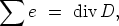
so daß
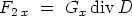 | (5a) |
wird. Die X-Komponente der von der elektrischen Feldstärke
auf die Volumeneinheit der Materie ausgeübten Kraft ist daher
gleich:
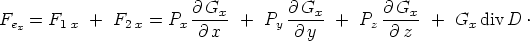 | (6) |
Analog erhalten wir unter Berücksichtigung der
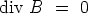
für die X-Komponente der von der magnetischen Feldstärke
gelieferten Kraft:
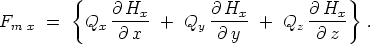 | (7) |