List of thumbnails
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
motorische Kraft maßgebend ist, denn im Innern des Streifens
ist die magnetische Induktion Bi gleich der außerhalb des
Streifens wirkenden Kraft Ha, unabhängig von dem Werte der
Permeabilität des Streifens, während die im Innern des Streifens
herrschende Kraft Hi bei gegebenem äußeren Felde von 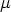
abhängt. Dieser Schluß ist aber nicht stichhaltig, weil die
ins Auge gefaßte ponderomotorische Kraft nicht die einzige
ist, welche auf unseren Materialstreifen wirkt. Das äußere
Feld Ha induziert nämlich auf der Oberseite und Unterseite
des Materialstreifens magnetische Belegungen von der Dichte1):
Ha 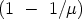 , und zwar auf der Oberseite eine negative, auf der
, und zwar auf der Oberseite eine negative, auf der
Unterseite eine positive Belegung. Auf jede dieser Belegungen
wirkt eine von dem im Streifen fließenden Strom erzeugte Kraft
von der Stärke i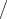 2 b pro Längeeinheit des Streifens2), welche
2 b pro Längeeinheit des Streifens2), welche
magnetische Kraft an der Oberseite und Unterseite verschieden
gerichtet ist. Die so resultierenden ponderomotorischen Kräfte
addieren sich, so daß wir die ponderomotorische Kraft erhalten:
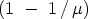 Ha i. Diese Kraft scheint bis jetzt nicht berück-
Ha i. Diese Kraft scheint bis jetzt nicht berück-
sichtigt worden zu
Die auf die Längeeinheit unseres Streifens im ganzen aus-
geübte Kraft ist nun gleich der Summe der soeben berech-
neten und der auf die Volumenelemente des Streifens infolge
des Stromdurchganges im Magnetfeld wirkenden Kraft R. Da
die gesamte auf die Längeeinheit wirkende ponderomotorische
Kraft erfahrungsgemäß gleich iHa ist, so besteht die
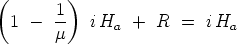
oder
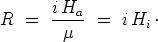
Man sieht also, daß für die Berechnung der ponderomotorischen
Kraft R, welche auf stromdurchflossene Volumenelemente
1) Die Dichte ist nämlich
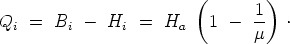
2) Statt dieser auf die Belegungen wirkenden Kräfte hätten wir
streng genommen nach den Resultaten des vorigen Paragraphen aller-
dings Volumenkräfte einführen müssen, was jedoch ohne Belang ist.