List of thumbnails
11 |
|
Dies muß als sehr unwahrscheinlich betrachtet werden.
Andererseits liefert uns die gewöhnliche Relativitätstheorie
kein Argument, aus dem wir folgern könnten, daß das Gewicht
eines Körpers von dessen Energieinhalt abhängt. Wir werden
aber zeigen, daß unsere Hypothese von der Äquivalenz der
Systeme K und K' die Schwere der Energie als notwendige
Konsequenz liefert. Es mögen sich die beiden mit Meßinstrumenten versehenen
körperlichen Systeme S1 und S2 in der Entfernung h von-
einander auf der z-Achse von K befinden 1), derart, daß das
Gravitationspotential in S2 um 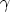 . h größer ist, als das in S1. Es
. h größer ist, als das in S1. Es
wurde von S2 gegen S1 eine bestimmte Energie-
E in Form von Strahlung gesendet. Die
Energiemengen mögen dabei in S1 und S2 mit
Vorrichtungen gemessen werden, die -- an einen
Ort des Systems z gebracht und dort mit-
einander verglichen -- vollkommen gleich seien.
Über den Vorgang dieser Energieübertragung
durch Strahlung läßt sich a priori nichts aus-
sagen, weil wir den Einfluß des Schwerefeldes
auf die Strahlung und die Meßinstrumente in S1 und S2 nicht
kennen. 
Nach unserer Voraussetzung von der Äquivalenz von K
und K' können wir aber an Stelle des im homogenen Schwere-
felde befindlichen Systems K das schwerefreie, im Sinne der
positiven z gleichförmig beschleunigt bewegte K' setzen,
mit dessen z-Achse die körperlichen Systeme S1 und S2 fest
verbunden
Den Vorgang der Energieübertragung durch Strahlung
von S2 auf S1
beurteilen wir von einem System K0 aus, das
beschleunigungsfrei sei. In bezug K0 besitze K' in dem
Augenblick die Geschwindigkeit Null, in welchem die Strah-
lungsenergie E2 von S2 gegen S1 abgesendet wird. Die Strah-
lung wird in S1
ankommen, wenn die Zeit h/c verstrichen ist
(in erster Annäherung). In diesem Momente besitzt aber S1
in bezug auf K0 die 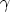 .h/c = v. Deshalb
.h/c = v. Deshalb
besitzt nach der gewöhnlichen Relativitätstheorie die in S1
1) S1 und S2 werden als gegenüber h unendlich klein betrachtet.