- Text
- Text Image
- Image
- XML
- Thumbnail overview
- Document information
ankommende Strahlung nicht die Energie E2, sondern eine
größere E1, welche mit E2 in erster Annäherung durch
die Gleichung verknüpft ist1
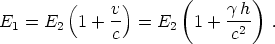 | (1) |
Nach unserer Annahme gilt genau die gleiche Beziehung,
falls derselbe Vorgang in dem nicht beschleunigten, aber mit
Gravitationsfeld versehenen System K stattfindet. In diesem
Falle können wir 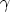 .h ersetzen durch das
.h ersetzen durch das  des
des
Gravitationsvektors in S2, wenn die willkürliche Konstante
von  in S1
gleich Null gesetzt wird. Es gilt also die
in S1
gleich Null gesetzt wird. Es gilt also die
Gleichung:
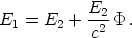 | (1 a) |
Diese Gleichung spricht den Energiesatz für den ins Auge
gefaßten Vorgang aus. Die in S1 ankommende Energie E1 ist
größer als die mit gleichen Mitteln gemessene Energie E2,
welche in S2 emittiert wurde, und zwar um die potentielle
Energie der Masse E2/c2 im Schwerefelde. Es zeigt sich
also, daß man, damit das Energieprinzip erfüllt sei, der
Energie E vor ihrer Aussendung in S2 eine potentielle Energie
der Schwere zuschreiben
muß, die der (schweren) Masse E/c2
entspricht. Unsere Annahme der Äquivalenz von K und K'
hebt also die am Anfang dieses Paragraphen dargelegte Schwierig-
keit, welche die gewöhnliche Relativitätstheorie übrig
Besonders deutlich zeigt sich der Sinn dieses Resultates
bei Betrachtung des folgenden
1. Man sendet die Energie E (in S2 gemessen) in Form
von Strahlung in S2 ab nach S1, wo nach dem soeben er-
langten Resultat die Energie E(1 + 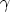 h/c2) aufgenommen wird
h/c2) aufgenommen wird
(in S1
2. Man senkt einen Körper W von der Masse M von S2
nach S1, wobei die Arbeit M 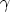 h nach außen abgegeben
h nach außen abgegeben
3. Man überträgt die Energie E von S1 auf den Körper W,
während sich W S1 befindet. Dadurch ädere sich die
schwere Masse M, so daß sie den Wert M'
1) A. Einstein, Ann. d. Phys. 17. p. 913 u. 914. 1905.