1
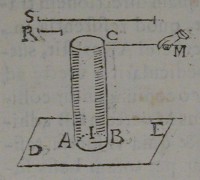
tiæ ad diuulſionem exercetur in centro I circuli AB.
Habebimus igitur vectem inflexum CBI in quo vis
mouens M applicatur in C, reſiſtentia verò applicatur
in I, & fulcimentum, ſeù centrum reuolutionis vectis
CBI eſt punctum B quod fixum perſeuerat dum cir
ca ipſum motus, & reuolutiones partium vectis fiunt;
Quaproptèr, iuxtà leges Mechanices, reſiſtentia to
talis ad diuulſionem, & ſeparationem ſuperficiei AB
ab ipſo pauimento ad vim mouentem M eamdem pro
portionem habebit, quam vectis longitudo CB ad
oppoſitam eius portionem BI, ſcilicèt habebit eam
dem proportionem. quam pondus S habet ad pondus
R. Verùm pondus R æquale erat potentiæ M. igitur
pondus S æquale erit reſiſtentię abſolutæ, & totali,
quam exercet ſuperficies AB quando diuelli, & ſe
parari debet à ſuperficie paui menti tractione directa.
Hinc deducitur quòd ſi pon
 71[Figure 71]
71[Figure 71]
dus O propoſitionis 89. di
uellit columnam à pauimento
directione, & impetu tranſ
uerſali, & perpendiculari ad
latus columnę, poterit nihilo
minùs indagari reſiſtentia ab
ſoluta, & totalis contiguita
tis, vel repugnantiæ ad vacuum earumdem ſuperfi
cierum, eritque talis vis abſoluta tantomaior pon
dere O, quantò altitudo columnæ CB maior eſt ſe
miſſe diametri AB, & ſic ſi vis transuerſalitèr colum
nam diuellens æqualis eſſet ponderi trium librarum
tiæ ad diuulſionem exercetur in centro I circuli AB.
Habebimus igitur vectem inflexum CBI in quo vis
mouens M applicatur in C, reſiſtentia verò applicatur
in I, & fulcimentum, ſeù centrum reuolutionis vectis
CBI eſt punctum B quod fixum perſeuerat dum cir
ca ipſum motus, & reuolutiones partium vectis fiunt;
Quaproptèr, iuxtà leges Mechanices, reſiſtentia to
talis ad diuulſionem, & ſeparationem ſuperficiei AB
ab ipſo pauimento ad vim mouentem M eamdem pro
portionem habebit, quam vectis longitudo CB ad
oppoſitam eius portionem BI, ſcilicèt habebit eam
dem proportionem. quam pondus S habet ad pondus
R. Verùm pondus R æquale erat potentiæ M. igitur
pondus S æquale erit reſiſtentię abſolutæ, & totali,
quam exercet ſuperficies AB quando diuelli, & ſe
parari debet à ſuperficie paui menti tractione directa.
Hinc deducitur quòd ſi pon
 71[Figure 71]
71[Figure 71]dus O propoſitionis 89. di
uellit columnam à pauimento
directione, & impetu tranſ
uerſali, & perpendiculari ad
latus columnę, poterit nihilo
minùs indagari reſiſtentia ab
ſoluta, & totalis contiguita
tis, vel repugnantiæ ad vacuum earumdem ſuperfi
cierum, eritque talis vis abſoluta tantomaior pon
dere O, quantò altitudo columnæ CB maior eſt ſe
miſſe diametri AB, & ſic ſi vis transuerſalitèr colum
nam diuellens æqualis eſſet ponderi trium librarum
