9589THEOR. ARITH.
autem corporis .M. miſti .vt .216. argentei verò .A. vt .156. detrahatur nunc pon-
dus .A. ex pondere .V. Reliquum erit .78. quod vocetur prima differentia ſeruan-
da, dematur etiam pondus .M. ex pondere .V. reliquum erit .18. pro ſecunda diffe-
rentia, etiam ſeruanda, multiplicetur poſteà pondus .A. per ſecundam differen-
tiam, productum verò diuidatur per primam differentiam. Vnde in præſenti exem
plo proueniet nobis .36. quiquidem prouentus erit quantitas argenti ipſius corpo-
ris miſti .M. quo etiam detracto ex pondere totali ipſius .M. reliquum erit quanti-
tas auri eius corporis, hoc eſt .180.
dus .A. ex pondere .V. Reliquum erit .78. quod vocetur prima differentia ſeruan-
da, dematur etiam pondus .M. ex pondere .V. reliquum erit .18. pro ſecunda diffe-
rentia, etiam ſeruanda, multiplicetur poſteà pondus .A. per ſecundam differen-
tiam, productum verò diuidatur per primam differentiam. Vnde in præſenti exem
plo proueniet nobis .36. quiquidem prouentus erit quantitas argenti ipſius corpo-
ris miſti .M. quo etiam detracto ex pondere totali ipſius .M. reliquum erit quanti-
tas auri eius corporis, hoc eſt .180.
In cuius operationis ſpeculatione, aliquid natura ſua prius cognitum præcedere
oportet hoc eſt, quod omnia corpora omogenea eandem proportionem obtinent
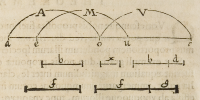
inter quantitates, quam inter pondera. Quo ſuppoſito denotetur corpus .A. li-
nea .o.a. corpus autem .V. linea .o.c. & corpus .M. linea .e.u: ſed .e.o. ſignificet par-
tem argenti, et .o.u. partem auri in corpore miſto .M. vnde ex communi conceptu
habebimus .o.e. æqualem .u.c. cum ex hypotheſi .e.u. æqualis ſit .o.c. et .a.o. ſimiliter.
Significetur poſteà pondus .a.o. ab .f. & pondus .e.u. ab .b.x. & pondus .o.c. ab .f.g. pon
dus verò .o.e. ab .b. pondus autem .o.u. ab .x. pondus enim .u.c. ab .b.d. et .g. ſit diffe-
rentia, qua .f.g. maior eſt .f: et .d.
 130[Figure 130]
differentia qua .b.d. maior eſt .b.
130[Figure 130]
differentia qua .b.d. maior eſt .b.
Vnde ex ratione omogeneitatis ea
dem proportio erit .a.o. ad .e.o. vt .
f. ad .b. et .o.c. ad .u.c. quæ .x.b.d. ſeu
f.g. (quodidem eſt) ad .b.d. Quare
ex .11. quinti eadem erit proportio .
f. ad .b. vt .f.g. ad .b.d. & permutan-
do ita erit .f. ad .f.g. vt .b. ad .b.d. &
ſeparando ita .f. ad .g. vt .b. ad .d. Sed .g. cognita nobis eſt, vt differentia in
ter .f. g, et .f: cognita nobis eſt etiam .f: cognoſcimus itidem .d. vt differentiam inter .
x.b.d. et .b.x. quapropter cognoſcemus .b. ex .20. ſeptimi Eucli. & ſic .x. reſiduum.
ex .b.x.
oportet hoc eſt, quod omnia corpora omogenea eandem proportionem obtinent
inter quantitates, quam inter pondera. Quo ſuppoſito denotetur corpus .A. li-
nea .o.a. corpus autem .V. linea .o.c. & corpus .M. linea .e.u: ſed .e.o. ſignificet par-
tem argenti, et .o.u. partem auri in corpore miſto .M. vnde ex communi conceptu
habebimus .o.e. æqualem .u.c. cum ex hypotheſi .e.u. æqualis ſit .o.c. et .a.o. ſimiliter.
Significetur poſteà pondus .a.o. ab .f. & pondus .e.u. ab .b.x. & pondus .o.c. ab .f.g. pon
dus verò .o.e. ab .b. pondus autem .o.u. ab .x. pondus enim .u.c. ab .b.d. et .g. ſit diffe-
rentia, qua .f.g. maior eſt .f: et .d.
Vnde ex ratione omogeneitatis ea
dem proportio erit .a.o. ad .e.o. vt .
f. ad .b. et .o.c. ad .u.c. quæ .x.b.d. ſeu
f.g. (quodidem eſt) ad .b.d. Quare
ex .11. quinti eadem erit proportio .
f. ad .b. vt .f.g. ad .b.d. & permutan-
do ita erit .f. ad .f.g. vt .b. ad .b.d. &
ſeparando ita .f. ad .g. vt .b. ad .d. Sed .g. cognita nobis eſt, vt differentia in
ter .f. g, et .f: cognita nobis eſt etiam .f: cognoſcimus itidem .d. vt differentiam inter .
x.b.d. et .b.x. quapropter cognoſcemus .b. ex .20. ſeptimi Eucli. & ſic .x. reſiduum.
ex .b.x.
THEOREMA CXXIII.
NVNC ex methodo præcedentis propoſiti deuenire poſſumus in cognitio-
nem veræ quantitatis auri, & argenti confuſi in corona Hieronis conſtituen-
do primum duo corpora ſimplicia æqualia inter ſe, & coronæ hoc modo videlicet,
immergendo coronam, ſeu corpus miſtum in aliquod vas aqua plenum, & diligen-
ter colligere aquam, quæ ex eo effundetur, poſteà verò oportet, aliud vas inuenire
præciſæ capax illius a quæ collectæ, in quod demum infundatur tantum auri, & po-
ſteà tantum argenti, quantum ſieri poteſt, vnde vnumquodque horum duorum cor
porum ſimplicium æquale erit mixto, ſeu coronæ, & ſic quod dictum eſt in præce-
cedenti theoremate exequemur.
nem veræ quantitatis auri, & argenti confuſi in corona Hieronis conſtituen-
do primum duo corpora ſimplicia æqualia inter ſe, & coronæ hoc modo videlicet,
immergendo coronam, ſeu corpus miſtum in aliquod vas aqua plenum, & diligen-
ter colligere aquam, quæ ex eo effundetur, poſteà verò oportet, aliud vas inuenire
præciſæ capax illius a quæ collectæ, in quod demum infundatur tantum auri, & po-
ſteà tantum argenti, quantum ſieri poteſt, vnde vnumquodque horum duorum cor
porum ſimplicium æquale erit mixto, ſeu coronæ, & ſic quod dictum eſt in præce-
cedenti theoremate exequemur.
THEOREMA CXXIIII.
SED vt breuiori methodo idem præſtemus, quod in antecedenti propoſito di-
ctum eſt, quædam theoremata præmittenda ſunt, videlicet quòd quotíeſcunque
fuerint tria corpora, quorum duo inuicem æqualia ſint in quantitate, ſed diuerſa-
ctum eſt, quædam theoremata præmittenda ſunt, videlicet quòd quotíeſcunque
fuerint tria corpora, quorum duo inuicem æqualia ſint in quantitate, ſed diuerſa-

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib