379367EPISTOL AE.
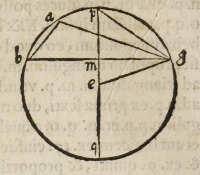
e .g. vnde angulus .g.e.q. æqualis erit angulo .b.a.g. portionis, cum duplus ſit angulo
q.p.g. medietati anguli ipſius portionis ex .19. tertij, ita quod angulus .q.e.g. nobis
cognitus erit, & ſimiliter arcus .g.q. & conſequenter ar-
cus .p.g. reſiduum medij circuli, & ſic .m.g. eius ſinus re
 419[Figure 419]
ctus, & etiam chorda .p.g. vt dupla ſinus dimidij arcus .
419[Figure 419]
ctus, & etiam chorda .p.g. vt dupla ſinus dimidij arcus .
p.g. & ſic .p.m. eius ſinus verſus, vel vt tertium latus trian
guli orthogonij .p.g.m. vnde nobis cognita erit propor
tio ipſius .b.g. (quæ dupla eſt ipſi .m.g.) ad .m.p. & quia
productum .p.m. in .m.q. æquale eſt ei, quod fit ex .b.m.
in m.g. ex .34. tertij, quapropter nobis cognita erit pars
q.m. quæ cum .p.m. complet totum diametrum .q.p. vn
de nobis cognita erit proportio ipſius .b.g. ad .q.p. qua
mediante cognoſcemus diametrum ſecundum partes il
las quibus propoſita ſuerit .b.g.
q.p.g. medietati anguli ipſius portionis ex .19. tertij, ita quod angulus .q.e.g. nobis
cognitus erit, & ſimiliter arcus .g.q. & conſequenter ar-
cus .p.g. reſiduum medij circuli, & ſic .m.g. eius ſinus re
p.g. & ſic .p.m. eius ſinus verſus, vel vt tertium latus trian
guli orthogonij .p.g.m. vnde nobis cognita erit propor
tio ipſius .b.g. (quæ dupla eſt ipſi .m.g.) ad .m.p. & quia
productum .p.m. in .m.q. æquale eſt ei, quod fit ex .b.m.
in m.g. ex .34. tertij, quapropter nobis cognita erit pars
q.m. quæ cum .p.m. complet totum diametrum .q.p. vn
de nobis cognita erit proportio ipſius .b.g. ad .q.p. qua
mediante cognoſcemus diametrum ſecundum partes il
las quibus propoſita ſuerit .b.g.
Hoc autem problema non in numeris ſed in continuo ab Euclid. ponitur in .32.
tertij.
tertij.
De inuentione alterius trianguli conditionati.
AD EVNDEM.
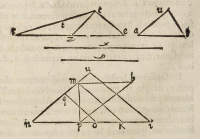
QVotieſcunque etiam inuenire voluerimus triangulum aliquem, puta .n.q.o.
æqualem triangulo .t. (exempli gratia) propoſito, qui habeat angulum .n. æ-
qualem angalo .a. dato, latera vero continentia ipſum angulum .n. ſint inuicem pro-
portionata vt .x. et .y. ita faciemus, accipiemus lineam .n.m. cuius volueris magnitu-
dinis, ſupra quam conſtituemus triangulum .m.n.p. æqualem triangulo .t. hac metho-
do, hoc eſt prolungando latus .r.z. trianguli .t. quod ſit .r.e. ita vt duplum ſit ipſi .r.z.
ducendo poſtea .c.e. habebimus ex .38. primi triangulum .t. eſſe dimidium totius
trianguli .r.c.e. deſignabimus deinde ex .44. dicti ſuperficiem .p.n.m.b. parallelo
grammam æqualemque; triangu
lo .r.c.e. habentem angulum .
 420[Figure 420]
n. æqualem angulo .a. ducatur
420[Figure 420]
n. æqualem angulo .a. ducatur
poſtea .p.m. & habebimus triam
gulum .m.n.p. æqualem .t. cum
angulo .n. æquali angulo .a. pro
ducatur poſtea .n.p. ita vt .n.K.
ſe habeat .ad .n.m. quemadmo
dum .x. ad .y. quod erit facilli-
mum producendo .n.m. et .n.
K. indeterminatè ſi oportuerit,
deinde eas ad æqualitatem ſe-
cando ipſis .x. et .y. efficiendo
exempli gratia quod .n.i. ſit
æqualis ipſi .x. et .n.u. ipſi .y. du
cendo poſtea .u.i. deinde à puncto .m. ducendo .m.K. æquidiſtanter .u.i. ex .31.
primi. & ſic habebimus ex .4. ſexti proportionem .x. ad .y. eſſe inter .n.K. et .n.
æqualem triangulo .t. (exempli gratia) propoſito, qui habeat angulum .n. æ-
qualem angalo .a. dato, latera vero continentia ipſum angulum .n. ſint inuicem pro-
portionata vt .x. et .y. ita faciemus, accipiemus lineam .n.m. cuius volueris magnitu-
dinis, ſupra quam conſtituemus triangulum .m.n.p. æqualem triangulo .t. hac metho-
do, hoc eſt prolungando latus .r.z. trianguli .t. quod ſit .r.e. ita vt duplum ſit ipſi .r.z.
ducendo poſtea .c.e. habebimus ex .38. primi triangulum .t. eſſe dimidium totius
trianguli .r.c.e. deſignabimus deinde ex .44. dicti ſuperficiem .p.n.m.b. parallelo
grammam æqualemque; triangu
lo .r.c.e. habentem angulum .
poſtea .p.m. & habebimus triam
gulum .m.n.p. æqualem .t. cum
angulo .n. æquali angulo .a. pro
ducatur poſtea .n.p. ita vt .n.K.
ſe habeat .ad .n.m. quemadmo
dum .x. ad .y. quod erit facilli-
mum producendo .n.m. et .n.
K. indeterminatè ſi oportuerit,
deinde eas ad æqualitatem ſe-
cando ipſis .x. et .y. efficiendo
exempli gratia quod .n.i. ſit
æqualis ipſi .x. et .n.u. ipſi .y. du
cendo poſtea .u.i. deinde à puncto .m. ducendo .m.K. æquidiſtanter .u.i. ex .31.
primi. & ſic habebimus ex .4. ſexti proportionem .x. ad .y. eſſe inter .n.K. et .n.
