3220I O. BAPT. BENED.
biturum, ſicut .u.x. ad .n.x. ex prima ſexti aut .18. vel .19. ſeptimi,
quare ex 11.
quinti ita ſe habebit .o.x. ad .e.x. ſicut .s.x. ad vnitatem; ſed ſicut ſe habet .s.x. ad.
vnitatem, ita ſe habet pariter .o.x. ad .m. vnde ex .11. prædicta ita ſe habebit .o.
x. ad .m. ſicut idipſum .o.x. ad .e.x. itaq́ue ex .9. prædicti quinti .m. æqualis erit .o.x.
quinti ita ſe habebit .o.x. ad .e.x. ſicut .s.x. ad vnitatem; ſed ſicut ſe habet .s.x. ad.
vnitatem, ita ſe habet pariter .o.x. ad .m. vnde ex .11. prædicta ita ſe habebit .o.
x. ad .m. ſicut idipſum .o.x. ad .e.x. itaq́ue ex .9. prædicti quinti .m. æqualis erit .o.x.
THEOREMA XXXI.
CVR propoſito aliquo numero in duas partes inæquales diuiſo, ſi rurſus per
quamlibet ipſarum diuidatur, prouenientia tantumdem coniuncta quantum
multiplicata efficiant.
quamlibet ipſarum diuidatur, prouenientia tantumdem coniuncta quantum
multiplicata efficiant.
Exempli gratia, ſit denarius prop oſitus numerus, per binarium & octonarium
diuiſus, prouenientia erunt quinque & vnum cum quarta parte, quæ coniuncta
crunt .6. cum quarta parte lineari, quæ ſi mul multiplicata, pariter erunt .6. cum
quarta parte ſuperficiali.
diuiſus, prouenientia erunt quinque & vnum cum quarta parte, quæ coniuncta
crunt .6. cum quarta parte lineari, quæ ſi mul multiplicata, pariter erunt .6. cum
quarta parte ſuperficiali.
Cuius ſpeculationis cauſa, totalis numerns, linea .q.p. ſignificetur, eius duæ
partes, per .k. maiorem et .u. minorem, ipſa vnitas per .t: proueniens ex diuiſio-
ne .q.p. per .k. ſit .q.i. proueniens autem ipſius .q.p. per .u. ſit .q.f. quare ex defini-
tione diuiſionis ita ſe habebit .q.p. ad .q.i. ſicut .k. ad .t. et .q.p. ad .q.f. ſicut .u. ad .t.
hoc eſt .q.f. ad .q.p. ſicut .t. ad .u. vnde ex æqualitate proportionum ſic ſe habebit .q.f.
ad .q.i. ſicut .k. ad .u. et conuerſim. Ad hæc in linea .q.p. vnitas, per lineam .q.o. ſigni-
ficetur, quo facto, dicamus, ſi .q.p. ad .q.i. ſic ſe habet vt .k. ad .q.o. itaque permu-
tando, ſic ſe habebit .q.p. ad .k. ſicut .q.i. ad .q.o. hoc eſt .k.u. ad .k. ſicut .i.q.f. ad .
q.f. (nam .k.u. partes ſunt integrales totius .q.p. et .k.u. ad .k. eſt ſicut .i.q.f. ad .q.f.
ex .18. quinti) Quare ita erit .i.q.f. ad .q.f. ſicut .q.i. ad vnitatem .q.o. ex .11. quinti
Addatur deinde .q.i. ad .q.f. et .q.i. per .
q.f. multiplicetur, cuius multiplicatio-
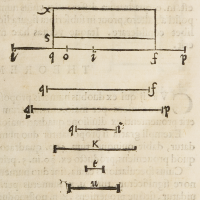 43[Figure 43]
nis productum, ſit .x.f. quod probabo
43[Figure 43]
nis productum, ſit .x.f. quod probabo
æquale eſſe ſummæ .f.q. cum .q.i. Sece-
tur enim linea .q.x. in puncto .s. ita. vt .
q.s. æqualis ſit .q.o. ſigneturq́ue pro-
ductum .s.f. quare eadem erit propor-
tio quantitatis .x.f. ad .s.f. quæ eſt .q.x.
ad .q.s. ex prima ſexti, aut .18. vel 19.
ſeptimi, hoc eſt, ſicut .q.i. ad .q.o. et
ex .11. quinti (vt dictum eſt) ſicut .i.q.
f. ad .q.f. ſed numerus .s.f. fuperficia-
lis tantus eſt, quantus linearis .q.f.
quare ex .9. quinti tantus erit (ſu-
perficialiter) numerus .x.f. quantus
(lineariter). f.q.i. quod erat pro-
poſitum.
partes, per .k. maiorem et .u. minorem, ipſa vnitas per .t: proueniens ex diuiſio-
ne .q.p. per .k. ſit .q.i. proueniens autem ipſius .q.p. per .u. ſit .q.f. quare ex defini-
tione diuiſionis ita ſe habebit .q.p. ad .q.i. ſicut .k. ad .t. et .q.p. ad .q.f. ſicut .u. ad .t.
hoc eſt .q.f. ad .q.p. ſicut .t. ad .u. vnde ex æqualitate proportionum ſic ſe habebit .q.f.
ad .q.i. ſicut .k. ad .u. et conuerſim. Ad hæc in linea .q.p. vnitas, per lineam .q.o. ſigni-
ficetur, quo facto, dicamus, ſi .q.p. ad .q.i. ſic ſe habet vt .k. ad .q.o. itaque permu-
tando, ſic ſe habebit .q.p. ad .k. ſicut .q.i. ad .q.o. hoc eſt .k.u. ad .k. ſicut .i.q.f. ad .
q.f. (nam .k.u. partes ſunt integrales totius .q.p. et .k.u. ad .k. eſt ſicut .i.q.f. ad .q.f.
ex .18. quinti) Quare ita erit .i.q.f. ad .q.f. ſicut .q.i. ad vnitatem .q.o. ex .11. quinti
Addatur deinde .q.i. ad .q.f. et .q.i. per .
q.f. multiplicetur, cuius multiplicatio-
æquale eſſe ſummæ .f.q. cum .q.i. Sece-
tur enim linea .q.x. in puncto .s. ita. vt .
q.s. æqualis ſit .q.o. ſigneturq́ue pro-
ductum .s.f. quare eadem erit propor-
tio quantitatis .x.f. ad .s.f. quæ eſt .q.x.
ad .q.s. ex prima ſexti, aut .18. vel 19.
ſeptimi, hoc eſt, ſicut .q.i. ad .q.o. et
ex .11. quinti (vt dictum eſt) ſicut .i.q.
f. ad .q.f. ſed numerus .s.f. fuperficia-
lis tantus eſt, quantus linearis .q.f.
quare ex .9. quinti tantus erit (ſu-
perficialiter) numerus .x.f. quantus
(lineariter). f.q.i. quod erat pro-
poſitum.
THEOREMA. XXXII.
CVR numero aliquo in duas partes inæquales diuiſo, ſi rurſus diuidatur per
ſingulas partes, ſumma duorum prouenientium per binarium, ſemper ma-
ior ſit ſumma prouenientium ex diuiſione vnius partis per alteram.
ſingulas partes, ſumma duorum prouenientium per binarium, ſemper ma-
ior ſit ſumma prouenientium ex diuiſione vnius partis per alteram.
Exempli gratia, ſi proponeretur numerus .24. qui in duas partes inæquales diuide

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib