5745THEOREM. ARIT.
componendo ſic ſe habebit .k.y. ad .m.y. ſicut .e.a. ad .o.a. & permutando .k.y. ad .e.
a. ſicut .m.y. ad .o.a. & ex .19. quinti ita .k.m. ad .e.o. ſicut .k.y. ad .e.a. & permutando .
k.m. ad .k.y. ſicut .e.o. ad .e.a. Nunc producatur .f.t. donec .t.i. æqualis ſit .k.y. produ-
ctaque; .m.t. done c.t.s. æqualis ſit vnitati .x. termineturque; rectangulum .s.i. ex quo da-
bitur proportio numeri .f.m. ad numerum .s.i. compoſita ex .m.t. ad .t.s. et .f.t. ad .t.i.
ex .24. ſexti, aut quinta octaui, ſed ita etiam proportio .q.b. ad .a.e. componitur ex
eiſdem proportionibus, nempe ex .q.b. ad .o.e. æquali .m.t. ad .t.s. & ex proportione .
o.e. ad .a.e. æquali .f.t. ad .t.i. ita que proportio numeri .f.m. ad .s.i. hoc eſt ad numerum
ipſius .k.y. ęqualis eſt proportioni numeri .q.b. ad .a.e. nempe .k.g. ad .k.u. hoc eſt .k.p. ad
x.y. ex quo ſequitur .k.p. conſtare numero ęquali .f.m. proueniens igitur ex diuiſione
numeri .k.z. per .f.m. æquale eſt numero ipſius .a.e.
a. ſicut .m.y. ad .o.a. & ex .19. quinti ita .k.m. ad .e.o. ſicut .k.y. ad .e.a. & permutando .
k.m. ad .k.y. ſicut .e.o. ad .e.a. Nunc producatur .f.t. donec .t.i. æqualis ſit .k.y. produ-
ctaque; .m.t. done c.t.s. æqualis ſit vnitati .x. termineturque; rectangulum .s.i. ex quo da-
bitur proportio numeri .f.m. ad numerum .s.i. compoſita ex .m.t. ad .t.s. et .f.t. ad .t.i.
ex .24. ſexti, aut quinta octaui, ſed ita etiam proportio .q.b. ad .a.e. componitur ex
eiſdem proportionibus, nempe ex .q.b. ad .o.e. æquali .m.t. ad .t.s. & ex proportione .
o.e. ad .a.e. æquali .f.t. ad .t.i. ita que proportio numeri .f.m. ad .s.i. hoc eſt ad numerum
ipſius .k.y. ęqualis eſt proportioni numeri .q.b. ad .a.e. nempe .k.g. ad .k.u. hoc eſt .k.p. ad
x.y. ex quo ſequitur .k.p. conſtare numero ęquali .f.m. proueniens igitur ex diuiſione
numeri .k.z. per .f.m. æquale eſt numero ipſius .a.e.
THEOREMA LXX.
HAEC porrò concluſio alia etiam via demonſtrari poteſt.
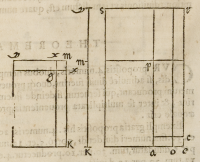
Significetur numerus diuidendus atque multiplicandus linea .b.a.
Deinde
diuidentes & multiplicantes ſint .k.m. et .m.y. prouenientia ex diuiſione ſint .a.o. et .o.
e. atque .a.o. ex .m.y: o.e. verò ex .k.m. proueniat, quorum ſumma ſit .a.e: productum
autem .b.a. in .k.m. ſit .b.p. et .p.s. productum .b.a. in .m.y. ad hæc rectangulum .k.y. ſit
productum .k.m. in .m.y: quo to-
tum productum .a.s. diuidatur, pro
 78[Figure 78]
ueniensque; ſit .a.c. cui, a.c: productum .
78[Figure 78]
ueniensque; ſit .a.c. cui, a.c: productum .
a.s. eandem proportionem ſeruabit, quam
k.y. rectangulum ad vnitatem ex
definitione diuiſionis, hoc autem
proueniens .a.c. conſtare numero æ-
quali aſſero ſummæ .a.e. Primum
enim ex dicta definitione diuiſio-
nis habemus eandem eſſe propor-
tionem .b.a. ad .a.o. quæ .m.y. ad
vnitatem, & quod ſic ſe habet .b.a.
ad .o.e. ſicut .k.m. ad eandem vnita
tem. Itaque vnitas hæc linearis ſi-
gnificetur per .m.x. in ſingulis late-
ribus .k.m. et .m.y. producentibus rectangulum .k.y: ſuperficialis autem vnitas ſit.
diuidentes & multiplicantes ſint .k.m. et .m.y. prouenientia ex diuiſione ſint .a.o. et .o.
e. atque .a.o. ex .m.y: o.e. verò ex .k.m. proueniat, quorum ſumma ſit .a.e: productum
autem .b.a. in .k.m. ſit .b.p. et .p.s. productum .b.a. in .m.y. ad hæc rectangulum .k.y. ſit
productum .k.m. in .m.y: quo to-
tum productum .a.s. diuidatur, pro
a.s. eandem proportionem ſeruabit, quam
k.y. rectangulum ad vnitatem ex
definitione diuiſionis, hoc autem
proueniens .a.c. conſtare numero æ-
quali aſſero ſummæ .a.e. Primum
enim ex dicta definitione diuiſio-
nis habemus eandem eſſe propor-
tionem .b.a. ad .a.o. quæ .m.y. ad
vnitatem, & quod ſic ſe habet .b.a.
ad .o.e. ſicut .k.m. ad eandem vnita
tem. Itaque vnitas hæc linearis ſi-
gnificetur per .m.x. in ſingulis late-
ribus .k.m. et .m.y. producentibus rectangulum .k.y: ſuperficialis autem vnitas ſit.

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib