363351EPISTOL AE.
Volo etiam quod ad partem .c.l.s. quadrilateri conſtituta ſit alia parallela ad .z.
r. & in æquali diſtantia ab ipſa quemadmodum .u.n. diſtat ad eademmet .z.r. ad ean
dem operationem faciendam. Vnde in vno tantummodo itinere puncti .s. ab .r. vſque;
ad .c. deſignabimus quartam partem ſectionis, conuerſo poſtea inſtrumento, hoc eſt
poſito puncto .r. vbi prius erat .z. et .z. vbi erat .r. aliam delineabimus quartam, &
ſic ad oppoſitam partem ipſius .z.r. faciendum erit. Hoc inſtrumentum poſſumus
etiam ita conſtruere, vt puncta .o. et .K. poſſint collocari in laterihus .c.e. et .e.s. vbi no
bis magis libuerit, ita vt licebit in qualibet proportione axium propoſita, oxygoniam
deſignare. Nam .c.o. erit longitudo dimidij axis minoris, et .c.e. dimidij maioris.
r. & in æquali diſtantia ab ipſa quemadmodum .u.n. diſtat ad eademmet .z.r. ad ean
dem operationem faciendam. Vnde in vno tantummodo itinere puncti .s. ab .r. vſque;
ad .c. deſignabimus quartam partem ſectionis, conuerſo poſtea inſtrumento, hoc eſt
poſito puncto .r. vbi prius erat .z. et .z. vbi erat .r. aliam delineabimus quartam, &
ſic ad oppoſitam partem ipſius .z.r. faciendum erit. Hoc inſtrumentum poſſumus
etiam ita conſtruere, vt puncta .o. et .K. poſſint collocari in laterihus .c.e. et .e.s. vbi no
bis magis libuerit, ita vt licebit in qualibet proportione axium propoſita, oxygoniam
deſignare. Nam .c.o. erit longitudo dimidij axis minoris, et .c.e. dimidij maioris.
DE CONSTITVTIONE TRIANGVLI
orthogonij conditionati.
orthogonij conditionati.
Domino Ludouico de Rocchaforte.
QVod à me poſtulas, non eſt admodum difficile, cupis enim triangulum
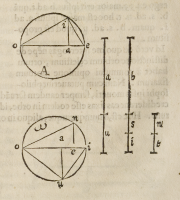
orthogonium, exempli gratia .o.i.e. in figura .A. ita conſtituere, vt di-
uiſum ſit à perpendiculari .a.i. & quod proportio .o.e. ad .o.i. ſit vt .o.i. ad
i.e. & quod quadrati .o.i. ad quadratum .o.a. ſit vt .e.i. ad .e.a. & quadra
tum .o.i. ad quadratum .e.i. ſit .ut .o.a. ad .e.a. Quæ omnia in promptu veniunt, quo
tieſcunque .o.e. fuerit diameter alicuius circuli, diuiſaque; in puncto .a. ſecundum pro
portionem habentem medium duoque; extrema, protracta deinde perpendiculari .a.
i. ad o.e. uſque ad circunferentiam, coniunctæque; .o.i. et .i.e: tale triangulum, omnia
ſupradicta in ſe continebit.
orthogonium, exempli gratia .o.i.e. in figura .A. ita conſtituere, vt di-
uiſum ſit à perpendiculari .a.i. & quod proportio .o.e. ad .o.i. ſit vt .o.i. ad
i.e. & quod quadrati .o.i. ad quadratum .o.a. ſit vt .e.i. ad .e.a. & quadra
tum .o.i. ad quadratum .e.i. ſit .ut .o.a. ad .e.a. Quæ omnia in promptu veniunt, quo
tieſcunque .o.e. fuerit diameter alicuius circuli, diuiſaque; in puncto .a. ſecundum pro
portionem habentem medium duoque; extrema, protracta deinde perpendiculari .a.
i. ad o.e. uſque ad circunferentiam, coniunctæque; .o.i. et .i.e: tale triangulum, omnia
ſupradicta in ſe continebit.
Nam ex .30. tertij angulus .i. rectus erit, & ex .8. ſexti .o.i. erit media proportio-
nalis inter .o.e. et .o.a. et .e.i. inter .o.e.
 400[Figure 400]
et .a.e. ſed quia ex diuiſione facta in pum
400[Figure 400]
et .a.e. ſed quia ex diuiſione facta in pum
cto .a. etiam .o.a. erit media proportio-
nalis inter totum & reſiduum, ideo ex .
11. quinti ita erit .o.e. ad .e.i. vt .o.e. ad .
o.a. vnde ex .9. eiuſdem .a.o. erit æqua-
lis .e.i. & ideo .o.i. erit media proportio
nalis inter .o.e. et .e.i. Sed quia propor-
tio .e.i. ad .a.e. eadem eſt, quę ipſius .o.e. ad
o.a. tunc videbis ex .18. ſexti, quod pro
portio quadrati .o.i. ad quadratum .o.a.
erit vt .e.i. ad .e.a. cum vero duo trian-
guli .o.i.a. et .a.i.e. ſint inuicem ſimiles
ex ſupradicta .8. ſexti, tunc videbis ex
18. et .17. eiuſdem dictos triangulos ean
dem habere inter ſe proportionem, quę
eſt inrer quadrata ipſius .o.i. et .i.e. vnde
ex prima ſexti ita ſe inuicem habebunt .
a.o. et .a.e.
nalis inter .o.e. et .o.a. et .e.i. inter .o.e.
cto .a. etiam .o.a. erit media proportio-
nalis inter totum & reſiduum, ideo ex .
11. quinti ita erit .o.e. ad .e.i. vt .o.e. ad .
o.a. vnde ex .9. eiuſdem .a.o. erit æqua-
lis .e.i. & ideo .o.i. erit media proportio
nalis inter .o.e. et .e.i. Sed quia propor-
tio .e.i. ad .a.e. eadem eſt, quę ipſius .o.e. ad
o.a. tunc videbis ex .18. ſexti, quod pro
portio quadrati .o.i. ad quadratum .o.a.
erit vt .e.i. ad .e.a. cum vero duo trian-
guli .o.i.a. et .a.i.e. ſint inuicem ſimiles
ex ſupradicta .8. ſexti, tunc videbis ex
18. et .17. eiuſdem dictos triangulos ean
dem habere inter ſe proportionem, quę
eſt inrer quadrata ipſius .o.i. et .i.e. vnde
ex prima ſexti ita ſe inuicem habebunt .
a.o. et .a.e.
Circa eam verò difficultatem quam
