365353EPISTOL AE.
DE MODO DIVIDENDI PARABOLAM
propoſitam ſecundum datam proportionem.
propoſitam ſecundum datam proportionem.
Pamphilo Gothfrid.
QVod à me quæris, eſt quidem poſſibile, non tamen adhuc inuentum, quo
niam nemo ad hunc vſque diem diuiſit vnam datam proportionem in tres
æquales partes, ſed ſi hoc pro facto conceſſeris, nunc tibi morem geram.
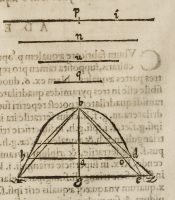
Nam proponis n. ihi parabolem .x.b.e. cum proportione .p. ad .q. cupiſque;
ſcire modum diuidendi ipſam parabolem vna mediante linea parallela ipſi baſi, ita
vt eandem habeat proportionem tota parabola ad partem abſciſſam, quæ eſt inter .
p. et .q. Ad quod faciendum, ſupponendum primò datam proportionem inter .
p. et .q. diuiſam eſſe in tres partes æquales, duabus lineis mediantibus .n. et .u. quæ me
diæ proportionales vocabuntur inter .p. et .q. deinde à quouis puncto circunferentię
ipſius figuræ ducatur parallela baſi .x.e. poſtea verò per puncta media harum dua-
rum æquidiſtantium protrahatur .g.b. quæ diameter erit ſectionis, ex 28. ſecundi Per-
gei, diuidatur deinde hæc diameter in puncto .a. ita quod eadem proportio ſit ipſius
b.g. ad .b.a. quæ ipſius .p. ad .u. quod tibi facile erit, ſecando à linea .p. partem .i. æqua
lem ipſi .u. tali modo poſtea diuidendo .b.g. ex .12. ſexti, ducatur a puncto .a. ipſa .d.
h. parallclam ipſi .x.e. & habebitur propoſitum.
niam nemo ad hunc vſque diem diuiſit vnam datam proportionem in tres
æquales partes, ſed ſi hoc pro facto conceſſeris, nunc tibi morem geram.
Nam proponis n. ihi parabolem .x.b.e. cum proportione .p. ad .q. cupiſque;
ſcire modum diuidendi ipſam parabolem vna mediante linea parallela ipſi baſi, ita
vt eandem habeat proportionem tota parabola ad partem abſciſſam, quæ eſt inter .
p. et .q. Ad quod faciendum, ſupponendum primò datam proportionem inter .
p. et .q. diuiſam eſſe in tres partes æquales, duabus lineis mediantibus .n. et .u. quæ me
diæ proportionales vocabuntur inter .p. et .q. deinde à quouis puncto circunferentię
ipſius figuræ ducatur parallela baſi .x.e. poſtea verò per puncta media harum dua-
rum æquidiſtantium protrahatur .g.b. quæ diameter erit ſectionis, ex 28. ſecundi Per-
gei, diuidatur deinde hæc diameter in puncto .a. ita quod eadem proportio ſit ipſius
b.g. ad .b.a. quæ ipſius .p. ad .u. quod tibi facile erit, ſecando à linea .p. partem .i. æqua
lem ipſi .u. tali modo poſtea diuidendo .b.g. ex .12. ſexti, ducatur a puncto .a. ipſa .d.
h. parallclam ipſi .x.e. & habebitur propoſitum.
Pro cuius reiratione, ſcies primum quod .h.d. diuiſa erit à diametro .b.g. per æqua
lia ex .7. primi Pergei, vel ſi cogitabimus aliquam lineam tangentem ipſam parabo
lam in puncto .b. tunc ex quinta ſecundi ipſius Pergei habebimus ipſam eſſe paralle-
lam .e.x. & ex .30. primi Eucli. erit ſimiliter æquidiſtans .d.h. vnde ex .46. primi eiuſ-
dem Pergei .h.a. æqualis erit .d.a. Protrahatur deinde .e.b: d b: x.b. et .h.b. vnde ex .17
lib. de quadratura parabolæ Archimedis, habebimus eandem proportionem ſuper
ficiei totalis parabolæ .x.b.e. ad trigonum .x.b.e. quæ portionis .h.b.d. ad ſuum tri-
gonum, eo quod tam vna quàm alia erit ſeſquitertia, eius etiam medietates ſic ſe habebunt.
lia ex .7. primi Pergei, vel ſi cogitabimus aliquam lineam tangentem ipſam parabo
lam in puncto .b. tunc ex quinta ſecundi ipſius Pergei habebimus ipſam eſſe paralle-
lam .e.x. & ex .30. primi Eucli. erit ſimiliter æquidiſtans .d.h. vnde ex .46. primi eiuſ-
dem Pergei .h.a. æqualis erit .d.a. Protrahatur deinde .e.b: d b: x.b. et .h.b. vnde ex .17
lib. de quadratura parabolæ Archimedis, habebimus eandem proportionem ſuper
ficiei totalis parabolæ .x.b.e. ad trigonum .x.b.e. quæ portionis .h.b.d. ad ſuum tri-
gonum, eo quod tam vna quàm alia erit ſeſquitertia, eius etiam medietates ſic ſe habebunt.
Vnde permutando, proportio medietatis totalis parabolę ad medietatem partia
lem ipſius, æqualis erit proportioni trianguli
g.b.e. ad triangulum .a.b.d. ſed ex .20. primi
Pergei, eadem eſt proportio quadrati ipſius .
 402[Figure 402]
g.e. ad quadratum ipſius .a.d. quæ .b.g. ad .b.a.
402[Figure 402]
g.e. ad quadratum ipſius .a.d. quæ .b.g. ad .b.a.
hoc eſt, vt .g.e. ad .a.o. ex ſimilitudine triangu-
lorum, & quia .b.g. ad .b.a. eſt ſicut .p. ad .u. ita
igitur erit quadrati ipſius .g.e. ad quadratum
ipſeus .a.d. quare .g.e. ad .a.d. erit ut p. ad .n.
ex .18. ſexti Euclid. ſed cum ex .24. eiuſdem
proportio trianguli .b.g.e. ad triangulum .b.
a.d. compoſita ſit ex proportione .g.e. ad .a.
d. er. ex .g.b. ad .b.a. hoc eſt .g.e. ad .a.o. &
quia proportio .g.e. ad .a.o. æqualis eſt ei quæ .p.
ad. u ex .11. quinti Euclid. & proportio .g.e.
ad .a.d. æqualis eſt ei quæ .p. ad .n. hoc eſt vt .u.
ad .q. ergo proportio trianguli .b.g.e. ad trian-
gulum .b.a.d. compoſita erit ex ca quę .p. ad .u.
& ex ea quæ .u. ad .q. æqualis ergo erit ei, quæ
p. ad .q. & ita medietates parabolarum, & eorum dupla.
lem ipſius, æqualis erit proportioni trianguli
g.b.e. ad triangulum .a.b.d. ſed ex .20. primi
Pergei, eadem eſt proportio quadrati ipſius .
hoc eſt, vt .g.e. ad .a.o. ex ſimilitudine triangu-
lorum, & quia .b.g. ad .b.a. eſt ſicut .p. ad .u. ita
igitur erit quadrati ipſius .g.e. ad quadratum
ipſeus .a.d. quare .g.e. ad .a.d. erit ut p. ad .n.
ex .18. ſexti Euclid. ſed cum ex .24. eiuſdem
proportio trianguli .b.g.e. ad triangulum .b.
a.d. compoſita ſit ex proportione .g.e. ad .a.
d. er. ex .g.b. ad .b.a. hoc eſt .g.e. ad .a.o. &
quia proportio .g.e. ad .a.o. æqualis eſt ei quæ .p.
ad. u ex .11. quinti Euclid. & proportio .g.e.
ad .a.d. æqualis eſt ei quæ .p. ad .n. hoc eſt vt .u.
ad .q. ergo proportio trianguli .b.g.e. ad trian-
gulum .b.a.d. compoſita erit ex ca quę .p. ad .u.
& ex ea quæ .u. ad .q. æqualis ergo erit ei, quæ
p. ad .q. & ita medietates parabolarum, & eorum dupla.
