369357EPISTOL AE.
gulus .p.n.q. vnde ex methodo .56.
 407[Figure 407]
primi triangulorum Monteregij,
407[Figure 407]
primi triangulorum Monteregij,
cognoſcemus reliqua trianguli .
q.p.n. Conſtituendo poſtea angu-
lum .q.n.u. æqualem angulo .n.q.p.
propoſitum habebimus.
cognoſcemus reliqua trianguli .
q.p.n. Conſtituendo poſtea angu-
lum .q.n.u. æqualem angulo .n.q.p.
propoſitum habebimus.
Si etiam puncta .q.p. lineæ .q.p.
orizontali in eodem plano non exi
ſterent cum puncto .n. nihil refer-
ret, dummodo in pauimento notem
tur puncta .c.e. proxima .n. in ijſdem
ſuperficiebus triangulorum .n.o.p.
et .n.o.q. vnde .n.c. et .n.e. erunt com-
munes ſectiones dictarum ſuperficierum cum ſuperficie pauimenti ſupra quam fit
ſtatio.
orizontali in eodem plano non exi
ſterent cum puncto .n. nihil refer-
ret, dummodo in pauimento notem
tur puncta .c.e. proxima .n. in ijſdem
ſuperficiebus triangulorum .n.o.p.
et .n.o.q. vnde .n.c. et .n.e. erunt com-
munes ſectiones dictarum ſuperficierum cum ſuperficie pauimenti ſupra quam fit
ſtatio.
CONI RECTI DIVISIO A PLANO
parallelo baſi ſecundum datam proportionem.
parallelo baſi ſecundum datam proportionem.
Rapbaeli de Auria.
QVotiescvnqve volueris conum rectum diuidere à plano parallelo ba-
ſi ſecundum vnam datam proportionem, nullius tibi erit difficultatis, con
ceſſa tamen pro inuenta diuiſione cuiuſuis propoſitę proportionis per tres
æquales partes.
ſi ſecundum vnam datam proportionem, nullius tibi erit difficultatis, con
ceſſa tamen pro inuenta diuiſione cuiuſuis propoſitę proportionis per tres
æquales partes.
Sit exempli gratia conus rectus .a.b.c. ſecandus vt dictum eſt, accipiatur latus
ipſius, quod ſit .a.c. ipſumque; diuidatur in puncto .d. ſecundum illam proportionem
quam deſideras, hoc eſt ipſius .a.c. ad .a.d. quo facto, inter totum .a.c. et .a.d. inuenian
tur duæ lineæ proportionales, quarum maior ſit .a.i. tunc ſi conus .a.b.c. ſectus fue-
rit à plano per punctum .i. parallelo baſi, habebimus quod quærebamus.
ipſius, quod ſit .a.c. ipſumque; diuidatur in puncto .d. ſecundum illam proportionem
quam deſideras, hoc eſt ipſius .a.c. ad .a.d. quo facto, inter totum .a.c. et .a.d. inuenian
tur duæ lineæ proportionales, quarum maior ſit .a.i. tunc ſi conus .a.b.c. ſectus fue-
rit à plano per punctum .i. parallelo baſi, habebimus quod quærebamus.
Cuius rei ratio, primò eſt, quia quotieſcunque conus aliquis ſectus fuerit ab ali-
quo plano parallelo baſi ipſius, pars ſuperior ſimilis ſemper erit totali cono, quod
ita probo, cogitemus conum ſectum eſſe
à plano per axem .a.l. vnde ex .3. primi
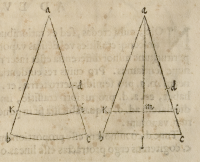 408[Figure 408]
Pergei, talis ſectio triangularis erit, quæ
408[Figure 408]
Pergei, talis ſectio triangularis erit, quæ
ſit .a.b.c. et .b.c. diameter erit baſis.
quo plano parallelo baſi ipſius, pars ſuperior ſimilis ſemper erit totali cono, quod
ita probo, cogitemus conum ſectum eſſe
à plano per axem .a.l. vnde ex .3. primi
ſit .a.b.c. et .b.c. diameter erit baſis.
Imaginemur deinde .K.i. communem
eſſe ſectionem huiuſmodi trianguli cum
plano parallelo ipſi baſi, tunc tale planum,
circulare erit ex .4. primi ipſius Pergei .K.
i. verò, eius diameter erit, et .a.m. ſuus axis.
eſſe ſectionem huiuſmodi trianguli cum
plano parallelo ipſi baſi, tunc tale planum,
circulare erit ex .4. primi ipſius Pergei .K.
i. verò, eius diameter erit, et .a.m. ſuus axis.
Cum verò .a.l. ſit perpendicularis ipſi
baſi conitotalis, eo quod rectus ſupponi-
tur, ideo eadem .a.m.l. erit perpendicula
ris eriam ipſi ſecundo plano circulari, ex
conuerſa .14. vndecimi Euclid. vnde ex
baſi conitotalis, eo quod rectus ſupponi-
tur, ideo eadem .a.m.l. erit perpendicula
ris eriam ipſi ſecundo plano circulari, ex
conuerſa .14. vndecimi Euclid. vnde ex
